
分析 (1)根据负整数指数幂、锐角三角函数和零指数幂可以解答本题;
(2)根据分式的除法和减法可以解答本题.
解答 解:(1)$\sqrt{4}$+($\frac{1}{2}$)-1-2cos60°+(2-π)0
=2+2-2×$\frac{1}{2}$+1
=2+2-1+1
=4;
(2)$\frac{{x}^{2}-1}{{x}^{2}+x}$÷(x-$\frac{2x-1}{x}$)
=$\frac{(x+1)(x-1)}{x(x+1)}×\frac{x}{{x}^{2}-2x+1}$
=$\frac{(x+1)(x-1)}{x(x+1)}×\frac{x}{(x-1)^{2}}$
=$\frac{1}{x-1}$.
点评 本题考查分式的混合运算、实数的运算、锐角三角函数、零指数幂、负整数指数幂,解答本题的关键是明确它们各自的计算方法.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
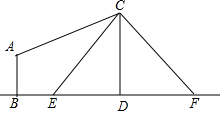 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
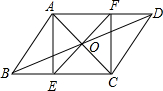 如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.
如图,在?ABCD中,AC,BD相交于点O,AE⊥BC,垂足为E,EO的延长线交AD于点F,请你猜想四边形AECF是怎样的四边形?证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com