
 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.分析 (1)由“CD⊥AB,EF⊥AB”可得出∠CDB=∠EFB=90°,再由“同位角相等,两直线平行”即可得出结论;
(2)由CD∥EF可得出∠2=∠BCD,再由∠1和∠2的关系可得出∠1=∠BCD,根据“内错角相等,两直线平行”即可得出DG∥BC,从而得出∠ACB=∠3=115°.
解答 (1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDB=90°,∠EFB=90°,
∴∠CDB=∠EFB=90°,
∴CD∥EF.
(2)解:∵CD∥EF,
∴∠2=∠BCD,
又∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠ACB=∠3=115°
点评 本题考查了平行线的判定及性质,解题的关键是根据同位角(内错角)相等证出两直线平行.本题属于基础题,难度不大,解决该题型题目时,根据角的关系证出直线平行是关键.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
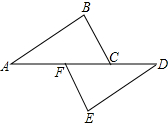 如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.
如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
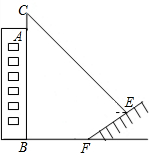 如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
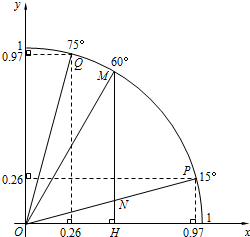 如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:
如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com