
 如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.
如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形. 分析 首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的等积转换可得邻边相等,则重叠部分为菱形.
解答 证明:∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,
∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);
过点D分别作AB,BC边上的高为DE,DF.如图所示:
则DE=DF(两纸条相同,纸条宽度相同);
∵平行四边形ABCD的面积=AB×DE=BC×DF,
∴AB=BC.
∴平行四边形ABCD为菱形(一组邻边相等的平行四边形是菱形).
点评 本题考查了菱形的判定、平行四边形的判定、菱形面积的计算;熟练掌握菱形的判定方法,由面积得出AB=BC是解决问题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
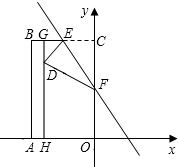 如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(-4,6),点E是BC的中点,点H在OA上,且AH=1,过点H且平行于y轴的HG与EB交于点G,现将矩形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,点F为折痕与y轴的交点.CF=2$\sqrt{3}$.
如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(-4,6),点E是BC的中点,点H在OA上,且AH=1,过点H且平行于y轴的HG与EB交于点G,现将矩形折叠,使顶点C落在HG上,并与HG上的点D重合,折痕为EF,点F为折痕与y轴的交点.CF=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com