
分析 题设中已知数较少,只知道周长为18,应抓住不等边三角形的边长都是整数这一条件,依据三角形三边关系先确定出最大边的取值范围,则问题迎刃而解.
解答 解:设 a<b<c,则a+b+c>2c,即 2c<18,所以 c<9.
因为a,b,c 都是正整数,所以若c=3,则其他两边必然为a=1,b=2.
由于1+2=3,即 a+b=c,故线段a,b,c不可能组成三角形.
当然c 更不可能为1或2,因而有4≤c<9.
当c=4时,a=2,b=3,不符合条件;
当c=5时,a=3,b=4,不符合条件;
当c=6时,a=4,b=5,不符合条件.
当c=7时,a=5,b=6,符合条件.
当c=8时,a=4,b=6,符合条件.
点评 本题考查了三角形的三边关系,关键是根据三角形三边关系确定出最大边的取值范围.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
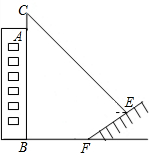 如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
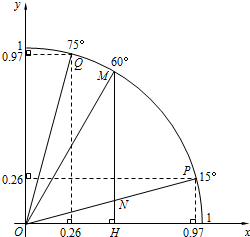 如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:
如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
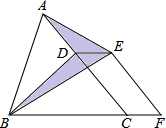 如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )| A. | 8 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com