
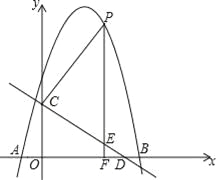
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉСНЕуЃЌжБЯпy=Љ![]() x+3гыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуDЃЎЕуPЪЧxжсЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛжБЯпCDгкЕуEЃЎЩшЕуPЕФКсзјБъЮЊmЃЎ
x+3гыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуDЃЎЕуPЪЧxжсЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPFЁЭxжсгкЕуFЃЌНЛжБЯпCDгкЕуEЃЎЩшЕуPЕФКсзјБъЮЊmЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєPE=5EFЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉШєЕуEЁфЪЧЕуEЙигкжБЯпPCЕФЖдГЦЕуЁЂЪЧЗёДцдкЕуPЃЌЪЙЕуEЁфТфдкyжсЩЯЃПШєДцдкЃЌЧыжБНгаДГіЯргІЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2+4x+5ЃЎЃЈ2ЃЉm=2Лђm=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉРэгЩМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉгУКЌmЕФДњЪ§ЪНЗжБ№БэЪОГіPEЁЂEFЃЌШЛКѓСаЗНГЬЧѓНтЃЛ
ЃЈ3ЃЉНтЬтЙиМќЪЧЪЖБ№ГіЕБЫФБпаЮPECEЁфЪЧСтаЮЃЌШЛКѓИљОнPE=CEЕФЬѕМўЃЌСаГіЗНГЬЧѓНтЃЛЕБЫФБпаЮPECEЁфЪЧСтаЮВЛДцдкЪБЃЌPЕуyжсЩЯЃЌМДПЩЕУЕНЕуPзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯпy=Љx2+bx+cгыxжсНЛгкA ЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉСНЕуЃЌ
Ёр![]() НтЕУ
НтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2+4x+5ЃЎ
ЃЈ2ЃЉЁпЕуPЕФКсзјБъЮЊmЃЌ
ЁрPЃЈmЃЌЉm2+4m+5ЃЉЃЌEЃЈmЃЌЉ![]() m+3ЃЉЃЌFЃЈmЃЌ0ЃЉЃЎ
m+3ЃЉЃЌFЃЈmЃЌ0ЃЉЃЎ
ЁрPE=|yPЉyE|=|ЃЈЉm2+4m+5ЃЉЉЃЈЉ![]() m+3ЃЉ|=|Љm2+
m+3ЃЉ|=|Љm2+![]() m+2|ЃЌ
m+2|ЃЌ
EF=|yEЉyF|=|ЃЈЉ![]() m+3ЃЉЉ0|=|Љ
m+3ЃЉЉ0|=|Љ![]() m+3|ЃЎ
m+3|ЃЎ
гЩЬтвтЃЌPE=5EFЃЌМДЃК|Љm2+![]() m+2|=5|Љ
m+2|=5|Љ![]() m+3|=|Љ
m+3|=|Љ![]() m+15|
m+15|
ЂйШєЉm2+![]() m+2=Љ
m+2=Љ![]() m+15ЃЌећРэЕУЃК2m2Љ17m+26=0ЃЌ
m+15ЃЌећРэЕУЃК2m2Љ17m+26=0ЃЌ
НтЕУЃКm=2Лђm=![]() ЃЛ
ЃЛ
ЂкШєЉm2+![]() m+2=ЉЃЈЉ
m+2=ЉЃЈЉ![]() m+15ЃЉЃЌећРэЕУЃКm2ЉmЉ17=0ЃЌ
m+15ЃЉЃЌећРэЕУЃКm2ЉmЉ17=0ЃЌ
НтЕУЃКm=![]() Лђm=
Лђm=![]() ЃЎ
ЃЎ
гЩЬтвтЃЌmЕФШЁжЕЗЖЮЇЮЊЃКЉ1ЃМmЃМ5ЃЌЙЪm=![]() ЁЂm==
ЁЂm==![]() етСНИіНтОљЩсШЅЃЎ
етСНИіНтОљЩсШЅЃЎ
Ёрm=2Лђm=![]() ЃЎ
ЃЎ
ЃЈ3ЃЉМйЩшДцдкЃЎ
зїГіЪОвтЭМШчЯТЃК
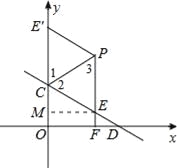
ЁпЕуEЁЂEЁфЙигкжБЯпPCЖдГЦЃЌ
ЁрЁЯ1=ЁЯ2ЃЌCE=CEЁфЃЌPE=PEЁфЃЎ
ЁпPEЦНаагкyжсЃЌЁрЁЯ1=ЁЯ3ЃЌ
ЁрЁЯ2=ЁЯ3ЃЌЁрPE=CEЃЌ
ЁрPE=CE=PEЁф=CEЁфЃЌМДЫФБпаЮPECEЁфЪЧСтаЮЃЎ
ЕБЫФБпаЮPECEЁфЪЧСтаЮДцдкЪБЃЌ
гЩжБЯпCDНтЮіЪНy=Љ![]() x+3ЃЌПЩЕУOD=4ЃЌOC=3ЃЌгЩЙДЙЩЖЈРэЕУCD=5ЃЎ
x+3ЃЌПЩЕУOD=4ЃЌOC=3ЃЌгЩЙДЙЩЖЈРэЕУCD=5ЃЎ
Й§ЕуEзїEMЁЮxжсЃЌНЛyжсгкЕуMЃЌвзЕУЁїCEMЁзЁїCDOЃЌ
Ёр![]() =
=![]() =ЃЌМД
=ЃЌМД![]() =
=![]() ЃЌНтЕУCE=
ЃЌНтЕУCE=![]() |m|ЃЌ
|m|ЃЌ
ЁрPE=CE=![]() |m|ЃЌгжгЩЃЈ2ЃЉПЩжЊЃКPE=|Љm2+
|m|ЃЌгжгЩЃЈ2ЃЉПЩжЊЃКPE=|Љm2+![]() m+2|
m+2|
Ёр|Љm2+![]() m+2|=
m+2|=![]() |m|ЃЎ
|m|ЃЎ
ЂйШєЉm2+![]() m+2=
m+2=![]() mЃЌећРэЕУЃК2m2Љ7mЉ4=0ЃЌНтЕУm=4Лђm=Љ
mЃЌећРэЕУЃК2m2Љ7mЉ4=0ЃЌНтЕУm=4Лђm=Љ![]() ЃЛ
ЃЛ
ЂкШєЉm2+![]() m+2=Љ
m+2=Љ![]() mЃЌећРэЕУЃКm2Љ6mЉ2=0ЃЌНтЕУm1=3+
mЃЌећРэЕУЃКm2Љ6mЉ2=0ЃЌНтЕУm1=3+![]() ЃЌm2=3Љ
ЃЌm2=3Љ![]() ЃЎ
ЃЎ
гЩЬтвтЃЌmЕФШЁжЕЗЖЮЇЮЊЃКЉ1ЃМmЃМ5ЃЌЙЪm=3+![]() етИіНтЩсШЅЃЎ
етИіНтЩсШЅЃЎ
ЕБЫФБпаЮPECEЁфЪЧСтаЮетвЛЬѕМўВЛДцдкЪБЃЌ
ДЫЪБPЕуКсзјБъЮЊ0ЃЌEЃЌCЃЌE'Ш§ЕужиКЯгыyжсЩЯЃЌвВЗћКЯЬтвтЃЌ
ЁрPЃЈ0ЃЌ5ЃЉ
злЩЯЫљЪіЃЌДцдкТњзуЬѕМўЕФЕуPзјБъЮЊЃЈ0ЃЌ5ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ4ЃЌ5ЃЉЛђЃЈ3Љ
ЃЉЛђЃЈ4ЃЌ5ЃЉЛђЃЈ3Љ![]()
2![]() Љ3ЃЉЃЎ
Љ3ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
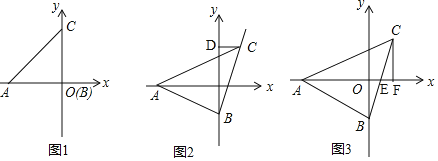
ЁОЬтФПЁПвбжЊЃЌЁїABCТњзуBCЃНABЃЌЁЯABCЃН90ЁуЃЌAЕудкxжсЕФИКАыжсЩЯЃЌжБНЧЖЅЕуBдкyжсЩЯЃЌЕуCдкxжсЩЯЗНЃЎ
ЃЈ1ЃЉШчЭМ1ЫљЪОЃЌШєAЕФзјБъЪЧЃЈЃ3ЃЌ0ЃЉЃЌЕуBгыдЕужиКЯЃЌдђЕуCЕФзјБъЪЧ_________ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуCзїCDЁЭyжсгкDЃЌЧыХаЖЯЯпЖЮOAЁЂODЁЂCDжЎМфЕФЪ§СПЙиЯЕВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєxжсЧЁКУЦНЗжЁЯBACЃЌBCгыxжсНЛгкЕуEЃЌЙ§ЕуCзїCFЁЭxжсгкЕуFЃЌЮЪCFгыAEгадѕбљЕФЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуЕФНсЙћЪЧa6ЕФЮЊЃЈЁЁЁЁЃЉ
A. a12ЁТa2B. a7ЉaC. a2a4D. ЃЈЉa2ЃЉ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊБугкЙмРэгыГЁЕиАВХХЃЌЫЩББФГжабЇаЃвдаЁУїЫљдкАрМЖЮЊР§ЃЌЖдбЇЩњВЮМгИїИіЬхг§ЯюФПНјааСЫЕїВщЭГМЦЃЎВЂАбЕїВщЕФНсЙћЛцжЦСЫШчЭМЫљЪОЕФВЛЭъШЋЭГМЦЭМЃЌЧыФуИљОнЯТСааХЯЂЛиД№ЮЪЬтЃК

ЃЈ1ЃЉдкетДЮЕїВщжаЃЌаЁУїЫљдкЕФАрМЖВЮМгРКЧђЯюФПЕФЭЌбЇгаЖрЩйШЫЃПВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉШчЙћбЇаЃга800УћбЇЩњЃЌЧыЙРМЦШЋаЃбЇЩњжагаЖрЩйШЫВЮМгРКЧђЯюФПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
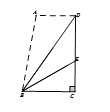
ЁОЬтФПЁПШчЭМЃЌЬнаЮABCDжаЃЌADЁЮBCЃЌDCЁЭBCЃЌНЋЬнаЮбиЖдНЧЯпBDелЕўЃЌЕуAЧЁКУТфдкDCБпЩЯЕФЕуEДІЃЌШєЁЯEBC=20ЁуЃЌдђЁЯEBDЕФЖШЪ§ЮЊ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЯУНјЛѕдБдЄВтвЛжжгІМОГФЩРФмГЉЯњЪаГЁЃЌОЭгУ0.8ЭђдЊЙКНјетжжГФЩРЃЌУцЪаКѓЙћШЛЙЉВЛгІЧѓЃЎгкЪЧЃЌЩЬЯУгжгУ1.76ЭђдЊЙКНјСЫЕкЖўХњетжжГФЩРЃЌЫљЙКЪ§СПЪЧЕквЛХњЙКНјЪ§СПЕФ2БЖЃЌЕЋЕЅМлЙѓСЫ4дЊЃЌЩЬЯУЯњЪлетжжГФЩРЪБУПМўдЄЖЈЪлМлЖМЪЧ58дЊЃЎ
ЃЈ1ЃЉЧѓетжжГФЩРдНјМлЮЊУПМўЖрЩйдЊЃП
ЃЈ2ЃЉОЙ§вЛЖЮЪБМфЯњЪлЃЌИљОнЪаГЁБЅКЭЧщПіЃЌЩЬЯУОРэОіЖЈЖдЪЃгрЕФ100МўГФЩРНјааДђелЯњЪлЃЌвдЬсИпЛиПюЫйЖШЃЌвЊЪЙетСНХњГФЩРЕФзмРћШѓВЛЩйгк6300дЊЃЌзюЖрПЩвдДђМИелЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫдкЯрЭЌЬѕМўЯТИїЩфАа10ДЮ,УПДЮЩфАаЕФГЩМЈЧщПіШчЭМЫљЪО:
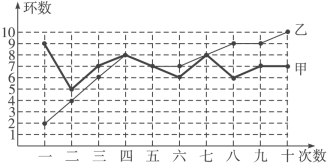
(1)ЧыЬюаДЯТБэ:
ЦНОљЪ§ | ЗНВю | жаЮЛЪ§ | Уќжа9ЛЗМАвдЩЯЕФДЮЪ§ | |
Мз | 7 | 1.2 | 1 | |
вв | 5.4 |
(2)ЧыДгЯТСаЫФИіВЛЭЌЕФНЧЖШЖдетДЮВтЪдНсЙћНјааЗжЮі:
ЂйДгЦНОљЪ§КЭЗНВюЯрНсКЯПД;
ЂкДгЦНОљЪ§КЭжаЮЛЪ§ЯрНсКЯПД(ЗжЮіЫЕФГЩМЈКУаЉ);
ЂлДгЦНОљЪ§КЭУќжа9ЛЗвдЩЯЕФДЮЪ§ЯрНсКЯПД(ЗжЮіЫЕФГЩМЈКУаЉ);
ЂмДгелЯпЭМЩЯСНШЫЩфЛїУќжаЛЗЪ§ЕФзпЪЦПД(ЗжЮіЫИќгаЧБСІ).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУМгМѕЯћдЊЗЈНтЯТСаЗНГЬ
ЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]()
ЃЈ3ЃЉ![]() ЃЈ4ЃЉ
ЃЈ4ЃЉ![]()
ЃЈ5ЃЉ ![]() ЃЈ6ЃЉ
ЃЈ6ЃЉ ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com