
如图,抛物线y=-x2+bx+c与直线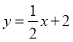 交于C、D两点,其中点C在y轴上,点D的坐标为(3,
交于C、D两点,其中点C在y轴上,点D的坐标为(3, ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F。
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F。
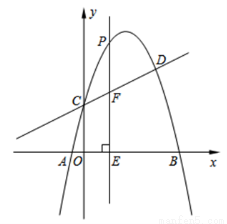
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源:2014-2015学年山东省九年级中考第三次模拟数学试卷(解析版) 题型:解答题
如图,把长为40cm,宽为30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为x cm.(纸板的厚度忽略不计)

(1)长方体盒子的长、宽、高分别为 (单位:cm);
(2)若折成的一个长方体盒子的表面积为950cm2,求此时长方体盒子的体积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级学业水平5月模拟考数学试卷(解析版) 题型:选择题
一艘轮船在同一航线上往返于甲、乙两地.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为 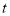 (h),航行的路程为
(h),航行的路程为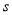 (km),则
(km),则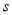 与
与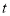 的函数图象大致是
的函数图象大致是
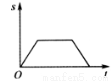
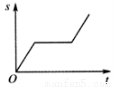
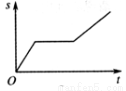
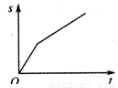
A B C D
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省陵县九年级学业水平考试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省陵县九年级学业水平考试数学试卷(解析版) 题型:选择题
已知边长为a的正方形的面积为8,则下列说法中,错误的是( )
A.a是无理数 B.a是方程x2﹣8=0的解
C.a是8的算术平方根 D.a满足不等式组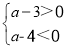
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级下学期学业水平模拟考试数学试卷(解析版) 题型:解答题
(1)解方程: 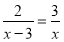
(2)(4分)如图,AB与⊙O相切于点B,连接AO交⊙O于C,OC=BC=6,求AB.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省九年级下学期第六次限时训练数学试卷(解析版) 题型:解答题
已知抛物线C1的函数解析式为y=ax2+bx-3a(b<0),若抛物线C1经过点(0,-3),方程ax2+bx-3a=0的两根为x1,x2,且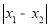 =4.
=4.
(1)求抛物线C1的顶点坐标.
(2)已知实数x>0,请证明x+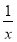 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+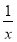 =2.
=2.
(3)若将抛物线C1先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90°,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S最小值及S取最小值时直线OA的函数解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省营口中考模拟考试二数学试卷(解析版) 题型:选择题
已知二次函数 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:
① 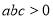 ;②
;② 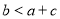 ; ③
; ③ 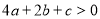 ;④
;④ 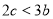 ;⑤
;⑤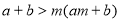 ,(
,(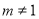 的实数)
的实数)
其中正确的结论有( )

A.2个 B.3个 C.4个 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com