
【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: ![]() ≈1.41).
≈1.41).
【答案】解:作EF⊥AC,
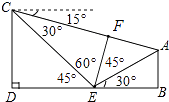
根据题意,CE=18×15=270米,
∵tan∠CED=1,
∴∠CED=∠DCE=45°,
∵∠ECF=90°-45°-15°=30°,
∴EF= ![]() CE=135米,
CE=135米,
∵∠CEF=60°,∠AEB=30°,
∴∠AEF=180°-45°-60°-30°=45°,
∴AE=135 ![]()
∴AB= ![]() ×135
×135 ![]() ≈95.2米.
≈95.2米.
【解析】先根据路程的公式求出CE的长,作EF⊥AC,再根据直角三角形中,30°角所对的直角边等于斜边的一半,求出EF的长,再在△AEF中,利用解直角三角形求出AE的长,然后再根据直角三角形的性质求出AB的长。
【考点精析】关于本题考查的含30度角的直角三角形和特殊角的三角函数值,需要了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能得出正确答案.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣ ![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的解析式和tan∠BAC的值;
(2)在(1)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(-4,0)、(0,2),⊙C的圆心坐标为(0,-2),半径为2.若D是⊙C上的一个动点,射线AD与 ![]() 轴交于点E,则△ABE面积的最大值是 .
轴交于点E,则△ABE面积的最大值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() ,
,![]() 满足
满足![]() .
.
(1)求点![]() 与点
与点![]() 在数轴上对应的数
在数轴上对应的数![]() 和
和![]() ;
;
(2)现动点![]() 从点
从点![]() 出发,沿数轴向右以每秒
出发,沿数轴向右以每秒![]() 个单位长度的速度运动;同时,动点
个单位长度的速度运动;同时,动点![]() 从点
从点![]() 出发,沿数轴向左以每秒
出发,沿数轴向左以每秒![]() 个单位长度的速度运动,设点
个单位长度的速度运动,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
① 若点![]() 和点
和点![]() 相遇于点
相遇于点![]() , 求点
, 求点![]() 在数轴上表示的数;
在数轴上表示的数;
② 当点![]() 和点
和点![]() 相距
相距![]() 个单位长度时,直接写出
个单位长度时,直接写出![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,有下列说法:
①食堂离小明家0.4km;
②小明从食堂到图书馆用了3min;
③图书馆在小明家和食堂之间;
④小明从图书馆回家的平均速度是0.04km/min.
其中正确的有( )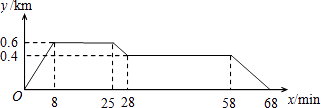
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,BC=2CD=2a,点E在边CD上,在矩形ABCD的左侧作矩形ECGF,使CG=2GF=2b,连接BD,CF,连结AF交BD于点H.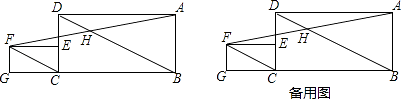
(1)求证:BD∥CF;
(2)求证:H是AF的中点;
(3)连结CH,若HC⊥BD,求a:b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com