Question

【题目】如图，已知A、B两点的坐标分别为（－4，0）、（0，2），⊙C的圆心坐标为（0，－2），半径为2．若D是⊙C上的一个动点，射线AD与 轴交于点E，则△ABE面积的最大值是 ．

Answer 1

【答案】
【解析】当射线AD与⊙C相切时，△ABE面积的最大．

如图，连接AC．

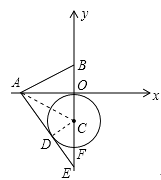
∵A点的坐标为（-4，0），⊙C的圆心坐标为（0，-2），半径为2．

∴AO=4，OC=2，即OC为⊙C的半径，则AO与⊙C相切．

∵AO、AD是⊙C的两条切线，

∴AD=AO=4．

连接CD，设EF=x，

∴DE2=EFOE，

∵CF=2，

∴DE= ．

易证△CDE∽△AOE，则 ，即 ，

解得x= 或x=0（不合题意，舍去），

∴BE=BO+OF+EF=2+4+ =

故△ABE面积的最大值为： = ．

【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点，需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．