
【题目】如图,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)你认为图b中的阴影部分的正方形的边长等于多少?
答:
(2)请用两种不同的方法求图b中阴影部分的面积.
方法1:
方法2:
(3)仔细观察图b,写出下列三个代数式之间的等量关系.
代数式:(m+n)2,(m-n)2,4mn
答:
(4)根据(3)题中所写的等量关系,解决如下问题.
若a+b=8,ab=5,则(a-b)2 = .
【答案】(1)边长为m-n;(2)(m+n)2-4mn和(m-n)2;(3)(m-n)2=(m+n)2-4mn;(4)44
【解析】
(1)观察得到长为m,宽为n的长方形的长宽之差即为阴影部分的正方形的边长;
(2)可以用大正方形的面积减去4个长方形的面积得到图b中的阴影部分的正方形面积;也可以直接利用正方形的面积公式得到;
(3)利用(2)中图b中的阴影部分的正方形面积得到(m-n)2=(m+n)2-4mn;
(4)根据(3)的结论得到(a-b)2=(a+b)2+4ab,然后把a+b=8,ab=5代入计算.
(1)图b中的阴影部分的正方形的边长等于长为m,宽为n的长方形的长宽之差,即m-n;
(2)方法一:图b中的阴影部分的正方形面积等于大正方形的面积减去4个长方形的面积,即(m+n)2-4mn;
方法二:图b中的阴影部分的正方形的边长等于m-n,所有其面积为(m-n)2;
(3)(m-n)2=(m+n)2-4mn;
(4)∵(a-b)2=(a+b)2-4ab,
当a+b=8,ab=5,
∴(a-b)2=82-4×5=44.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(-4,0)、(0,2),⊙C的圆心坐标为(0,-2),半径为2.若D是⊙C上的一个动点,射线AD与 ![]() 轴交于点E,则△ABE面积的最大值是 .
轴交于点E,则△ABE面积的最大值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图中提供的信息,有下列说法:
①食堂离小明家0.4km;
②小明从食堂到图书馆用了3min;
③图书馆在小明家和食堂之间;
④小明从图书馆回家的平均速度是0.04km/min.
其中正确的有( )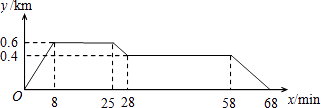
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com