
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

【答案】(1)30°;(2)①α=β,理由见解析;②当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.
【解析】试题分析:(1)证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;
(2)①证△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;
②α+β=180°或α=β,根据三角形外角性质求出即可.
试题解析:(1)解:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE.
在△BAD和△CAE中,∵AB=AC,∠BAD=∠CAE,AD=AE,∴△BAD≌△CAE(SAS),
∴∠B=∠ACE.
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE.
∵∠BAC=30°,∴∠DCE=30°.
故答案为:30°;
(2)解:当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β.理由是:
∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE.
在△BAD和△CAE中,∵AB=AC,∠BAD=∠CAE,AD=AE,∴△BAD≌△CAE(SAS),
∴∠B=∠ACE.
∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE.
∵∠BAC=α,∠DCE=β,∴α=β;

(3)解:当D在线段BC上时,α+β=180°,当点D在线段BC延长线或反向延长线上时,α=β.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7) 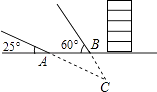
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:
(1).先化简,再求值:3a2+(4a2-2a-1)-2(3a2-a+1),其中a1![]()
(2). A=3a2+6ab-b2,B=2b2-5ab+a2,C=-4a2-ab+b2,先化简,再求值:A-[B-(A-B+3C)]-(A-B),其中 a=-0.2,b=-0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】早晨,小明步行到离家900米的学校去上学,到学校时发现眼镜忘在家中,于是他立即按原路步行回家,拿到眼镜后立即按原路骑自行车返回学校.已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟,小明骑自行车速度是步行速度的3倍.
(1)求小明步行速度(单位:米/分)是多少;
(2)下午放学后,小明骑自行车回到家,然后步行去图书馆,如果小明骑自行车和步行的速度不变,小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍,那么小明家与图书馆之间的路程最多是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.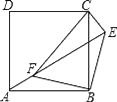
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,则下列判断错误的是( )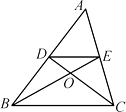
A.DE是△ABC的中位线
B.点O是△ABC的重心
C.△DEO∽△CBO
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6![]() ,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标.
,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标.
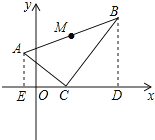
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣ ![]() ,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号).
,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号). 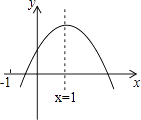
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com