
【题目】化简并求值:
(1)5(3a2b﹣ab2)﹣(ab2+3a2b),其中a=﹣![]() ,b=
,b=![]() .
.
(2)已知|x+1|+(y﹣2)2=0,求(2x2y﹣2xy2)﹣[(3x2y2+3x2y)+(3x2y2﹣3xy2)]的值.
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点P(x1,y1),Q(x2,y2),我们把|x1-x2|+|y1-y2|叫P,Q两点间的“平面距离”,记作d(P,Q)。
(1)已知O为坐标原点,动点M(x,y)是坐标轴上的点,满足d(O,M)=l,请写出点M的坐标。答: ________;
(2)设P0(x0,y0)是平面上一点,Q0(x,y)是直线l:y=kx+b上的动点,我们定义d(P0,Q0)的最小值叫做P0到直线l的“平面距离”。试求点M(2,1)到直线y=x+2的“平面距离”。
(3)在上面的定义基础上,我们可以定义平面上一条直线l与⊙C的“直角距离”:在直线l与⊙C上各自任取一点,此两点之间的“平面距离”的最小值称为直线l与⊙O的“平面距离”,记作d(l,⊙C)。
试求直线y=x+2与圆心在直角坐标系原点、半径是1的⊙O的直角距离d(l,⊙O)=__________。(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线a平行于x轴,且过点2,3和x,y,则y=________;
过点A2,5作x轴的垂线l,则直线l上的点的坐标特点是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下列程序计算,把答案填写在表格里,然后看看有什么规律,想想为什么会有
这个规律?
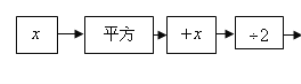

(1)填写表内空格:
输入 | 3 | 2 | -2 |
| … |
输出答案 | 0 | … |
(2)你发现的规律是____________.
(3)用简要过程说明你发现的规律的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便居民低碳出行,2016年10月1日起,聊城市公共自行车租赁系统(一期)试运行,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出)

请根据上面的统计图,解答下列问题:
(1)被调查的总人数是 ______ 人;
(2)公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?
(3)如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com