
【题目】如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=cm.
【答案】8
【解析】解:∵四边形ABCD是矩形,
∴AB=CD=15cm,∠A=∠D=90°,AD∥BC,AD=BC,
∴∠DEC=∠A′CB,
由折叠的性质,得:A′B=AB=15cm,∠BA′E=∠A=90°,
∴A′B=CD,∠BA′C=∠D=90°,
在△A′BC和△DCE中,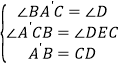 ,
,
∴△A′BC≌△DCE(AAS),
∴A′C=DE,
设A′C=xcm,则BC=AD=DE+AE=x+9(cm),
在Rt△A′BC中,BC2=A′B2+A′C2 ,
即(x+9)2=x2+152 ,
解得:x=8,
∴A′C=8cm.
故答案为:8.
由题意易证得△A′BC≌△DCE(AAS),BC=AD,A′B=AB=CD=15cm,然后设A′C=xcm,在Rt△A′BC中,由勾股定理可得BC2=A′B2+A′C2 , 即可得方程,解方程即可求得答案.


科目:初中数学 来源: 题型:
【题目】如图,已知直线l∥AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )

A. ①②④ B. ①③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若![]() ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图象的一部分.请根据图中信息,解答下列问题: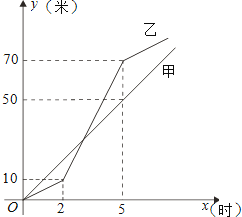
(1)①直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式;
②直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式;
(2)求开修几小时后,乙队修筑的水渠长度开始超过甲队?
(3)如果甲队施工速度不变,乙队在修筑5小时后,施工速度因故减少到5米/时,结果两队同时完成任务,求乙队从开修到完工所修水渠的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
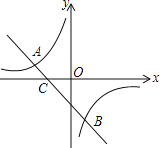
【题目】如图,已知A(﹣3,1),B(1, ![]() )是一次函数
)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出使一次函数的函数值小于反比例函数的函数值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据三视图求几何体的表面积.
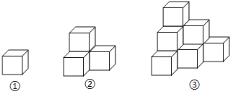
下列各图是棱长为![]() 的小正方体摆成的,如图①中,共有
的小正方体摆成的,如图①中,共有![]() 个小正方体,从正面看有
个小正方体,从正面看有![]() 个正方形,表面积为
个正方形,表面积为![]() ;如图②中,共有
;如图②中,共有![]() 个小正方体,从正面看有
个小正方体,从正面看有![]() 个正方形,表面积为
个正方形,表面积为![]() ;如图③,共有
;如图③,共有![]() 个小正方体,从正面看有
个小正方体,从正面看有![]() 个正方形,表面积为
个正方形,表面积为![]() ;…
;…
![]() 第
第![]() 个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?
个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?
![]() 第
第![]() 个图形中,从正面看有多少个正方形?表面积是多少?
个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东24.5°方向,轮船向正东航行了2400m,到达Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(参考数据cos41°=0.75).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com