
【题目】如图,已知直线l∥AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABCD的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BCA′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )

A. ①②④ B. ①③④ C. ①②③ D. ①②③④
【答案】D
【解析】分析:①根据平行四边形的判定方法可得到四边形ABCD为平行四边形,然后根据平行四边形的面积公式计算;②根据折叠的性质得到AC=CD,然后根据菱形的判定方法可判断四边形ABDC是菱形;③连结A′D,根据折叠性质和平行四边形的性质得到CA′=CA=BD,AB=CD=A′B,∠1=∠CBA=∠2,可证明△A′CD≌△A′BD,则∠3=∠4,然后利用三角形内角和定理得到得到∠1=∠4,则根据平行线的判定得到A′D∥BC;④讨论:当∠CBD=90°,则∠BCA=90°,由于S△A1CB=S△ABC=5,则S矩形A′CBD=10,根据勾股定理和完全平方公式进行计算;当∠BCD=90°,则∠CBA=90°,易得BC=2,而CD=5,于是得到结论.
详解:①∵AB=CD=5,AB∥CD,∴四边形ABCD为平行四边形,
∴四边形ABDC的面积=2×5=10;故①正确;
②∵四边形ABDC是平行四边形,∵A′与D重合时,∴AC=CD,
∵四边形ABDC是平行四边形,∴四边形ABDC是菱形;故②正确;
③连结A′D,如图,∵△ABC沿BC折叠得到△A′BC,
∴CA′=CA=BD,AB=CD=A′B, ∴△A′CD≌△A′BD(SSS),
∴∠3=∠4, 又∵∠1=∠CBA=∠2, ∴∠1+∠2=∠3+∠4, ∴∠1=∠4,
∴A′D∥BC, ∴∠CA′D+∠BCA′=180°;故③正确;
④设矩形的边长分别为a,b,当∠CBD=90°,∵四边形ABDC是平行四边形,
∴∠BCA=90°, ∴S△A′CB=S△ABC=5, ∴S矩形A′CBD=10,即ab=10, 而BA′=BA=5,
∴a2+b2=25, ∴(a+b)2=a2+b2+2ab=45, ∴a+b=![]() ;
;
当∠BCD=90°时, ∵四边形ABDC是平行四边形, ∴∠CBA=90°, ∴BC=2,
而CD=5, ∴(a+b)2=(2+5)2=49, ∴a+b=7,
∴此矩形相邻两边之和为![]() 或7,故④正确. 故选D.
或7,故④正确. 故选D.



科目:初中数学 来源: 题型:
【题目】△ABC中,BC=AC=5,AB=8,CD为AB边上的高,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面上滑动.如图2,设运动时间表为t秒,当B到达原点时停止运动.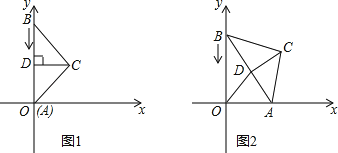
(1)当t=0时,求点C的坐标;
(2)当t=4时,求OD的长及∠BAO的大小;
(3)求从t=0到t=4这一时段点D运动路线的长;
(4)当以点C为圆心,CA为半径的圆与坐标轴相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.
(1)请写出一个六位连接数 ,它 (填“能”或“不能”)被13整除.
(2)是否任意六位连接数,都能被13整除,请说明理由.
(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=﹣ ![]() x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA.
x+b的图象经过点A(2,3),AB⊥x轴,垂足为B,连接OA. 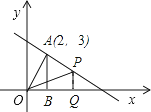
(1)求此一次函数的解析式;
(2)设点P为直线y=﹣ ![]() x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ=
x+b上的一点,且在第一象限内,经过P作x轴的垂线,垂足为Q.若S△POQ= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大众汽车经销商在销售某款汽车时,以高出进价20%标价.已知按标价的九折销售这款汽车9辆与将标价直降0.2万元销售4辆获利相同.
(1)求该款汽车的进价和标价分别是多少万元?
(2)若该款汽车的进价不变,按(1)中所求的标价出售,该店平均每月可售出这款汽车20辆;若每辆汽车每降价0.1万元,则每月可多售出2辆.求该款汽车降价多少万元出售每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义新运算;对于任意有理数![]() ,
,![]() ,都有
,都有![]() ,等式右边是通常的加法、减法及乘法运算,比如,数字
,等式右边是通常的加法、减法及乘法运算,比如,数字![]() 和
和![]() 在该新运算下结果为
在该新运算下结果为![]() ,计算如下:
,计算如下:
![]()
![]() 求
求![]() 的值;
的值;
![]() 任意有理数
任意有理数![]() ,
,![]() 请你重新定义一种新运算“
请你重新定义一种新运算“![]() ”,使得数字
”,使得数字![]() 和
和![]() 在你定义的新运算下运算的结果为
在你定义的新运算下运算的结果为![]() ;写出你定义的新运算________.
;写出你定义的新运算________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com