
����Ŀ��ij��������������������ij������ʱ���Ը߳�����20%��ۣ���֪����۵ľ��������������9���뽫���ֱ��0.2��Ԫ����4��������ͬ��
��1����ÿ������Ľ��ۺͱ�۷ֱ��Ƕ�����Ԫ��
��2�����ÿ������Ľ��۲��䣬����1��������ı�۳��ۣ��õ�ƽ��ÿ�¿��۳��������20������ÿ������ÿ����0.1��Ԫ����ÿ�¿ɶ��۳�2������ÿ��������۶�����Ԫ����ÿ�»��������������Ƕ��٣�
���𰸡�
��1��
�⣺�����Ϊx��Ԫ��������1.2x��Ԫ��������ã�
1.2x��0.9��9��9x=��1.2x��0.2����4��4x��
��ã�x=10��
1.2��10=12����Ԫ����
�𣺽���Ϊ10��Ԫ�����Ϊ12��Ԫ
��2��
�⣺��ÿ���������a��Ԫ������Ϊw��Ԫ��������ã�
w=��20+ ![]() ��2����12��10��a����
��2����12��10��a����
=��20��a�� ![]() ��2+45��
��2+45��
�ߩ�20��0��
�൱a= ![]() ʱ��w���=45��
ʱ��w���=45��
�𣺸ÿ���������0.5��Ԫ����ÿ�»���������������45��Ԫ
����������1�������Ϊx��Ԫ��������1.2x��Ԫ�����ݹؼ���䣺����۵ľ��������������9����������1.2x��0.9��9��9x�������ֱ��0.2��Ԫ����4�������ǣ�1.2x��0.2����4��4x������������ȿɵ÷���1.2x��0.9��9��9x=��1.2x��0.2����4��4x���ٽⷽ�̼��ɵõ����ۣ������õ���ۣ���2����ÿ���������a��Ԫ������Ϊw��Ԫ��������������ÿ������������=�������г�������ϵʽ���������䷽������ֵ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�EΪAB����һ�㣬����D��DF��DE����BC�ӳ��߽��ڵ�F������EF����CD�߽��ڵ�G����Խ���BD���ڵ�H��
��1����BF=BD=![]() ����BE�ij���
����BE�ij���
��2������ADE=2��BFE����֤��FH=HE+HD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������۹�˾����ijƷ��A��B������������֪A������ÿ������Ϊ![]() ��Ԫ��B������ÿ������Ϊ6��Ԫ��
��Ԫ��B������ÿ������Ϊ6��Ԫ��
![]() ��˾Ԥ���ò�����135��Ԫ�Ҳ�����129��Ԫ���ʽ�������������20�����м��ֽ������������Ƿֱ���ʲô��
��˾Ԥ���ò�����135��Ԫ�Ҳ�����129��Ԫ���ʽ�������������20�����м��ֽ������������Ƿֱ���ʲô��
![]() ���A������ÿ���ۼ�Ϊ9��Ԫ��B������ÿ���ۼ�Ϊ8��Ԫ��Ϊ��B����������·����˾����ÿ�۳�һ��B�������������˿��ֽ�a��Ԫ��Ҫʹ
���A������ÿ���ۼ�Ϊ9��Ԫ��B������ÿ���ۼ�Ϊ8��Ԫ��Ϊ��B����������·����˾����ÿ�۳�һ��B�������������˿��ֽ�a��Ԫ��Ҫʹ![]() �����еķ���������ͬ��aֵӦ�Ƕ��٣����ַ�����ʲô��(��ʾ�����蹺��B������x��)
�����еķ���������ͬ��aֵӦ�Ƕ��٣����ַ�����ʲô��(��ʾ�����蹺��B������x��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��AB��l��AB֮��ľ���Ϊ2��C��D��ֱ��l���������㣨��C��D�����ࣩ����AB=CD=5������AC��BC��BD������ABC��BC�۵��õ���A��BC������˵�������ı���ABCD�����ʼ��Ϊ10���ڵ�A����D�غ�ʱ���ı���ABDC�����Σ��۵�A����D���غ�ʱ������A�䡢D�����CA��D+��BCA��=180�㣻������A�䡢C��B��DΪ������ı���Ϊ���Σ���˾�����������֮��Ϊ3![]() ��7��������ȷ���ǣ�������
��7��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ۢ� C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����С����¥��D��20��B����һ�������ĵ��߸�AB������ô˵��߸���ˮƽ��DB�������Ϊ60�㣬��С����¥��C����õ��߸˶���A�ĸ���Ϊ30�㣬�ײ���B�ĸ���Ϊ45�㣨��A��B��D��C��ͬһƽ���ڣ�����֪���Ե�BΪԲ�ģ�10�׳�Ϊ�뾶��Բ����������һ���й㳡���йز�����Ѵ˵��߸�ˮƽ�ŵ�����B�㲻����Ϊ��ȫ�����������֪��������߸˷ŵ�����A�ܷ��������й㳡�ڣ���ͨ������ش�
�������ȷ��0.1�ף��ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��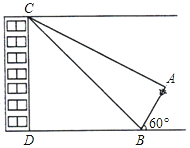
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ţ��ij��![]() ��ʼ��һ��������ֱ�����У��涨�����е�·�̼�Ϊ�������������е�·�̼�Ϊ�����������ĸ���·������Ϊ����λ�����ף���
��ʼ��һ��������ֱ�����У��涨�����е�·�̼�Ϊ�������������е�·�̼�Ϊ�����������ĸ���·������Ϊ����λ�����ף���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ͨ������˵����ţ�Ƿ�ص����
ͨ������˵����ţ�Ƿ�ص����![]() ��
��
![]() ��ţ�뿪������
��ţ�뿪������![]() ��Զʱ�Ƕ������ף�
��Զʱ�Ƕ������ף�
![]() �����й����У����ÿ��
�����й����У����ÿ��![]() ������
������![]() ��֥�飬����ţһ���õ�������֥�飿
��֥�飬����ţһ���õ�������֥�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������AOB����COD�У�OA=OB��OC=OD����AOB=��COD=90����
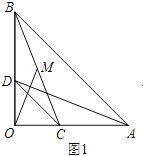
��1����ͼ1����C��D�ֱ��ڱ�OA��OB�ϣ�����AD��BC����MΪ�߶�BC���е㣬����OM���������ж��߶�AD��OM֮���������ϵ,������֤����
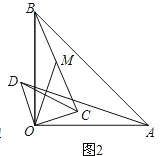
��2����ͼ2����ͼ1�е���COD�Ƶ�O��ʱ����ת����ת��Ϊ����0��������90����������AD��BC����MΪ�߶�BC���е㣬����OM�������жϣ�1���еĽ����Ƿ���Ȼ����������������֤����������������˵�����ɣ�
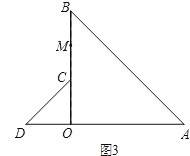
��3����ͼ3����ͼ1�е���COD�Ƶ�O��ʱ����ת��ʹ��COD��һ��ODǡ������AOB�ı�OA��ͬһ��ֱ����ʱ����C����OB�ϣ���MΪ�߶�BC���е㣮�����жϣ�1�����߶�AD��OM֮���������ϵ�Ƿ����仯��д����IJ��룬������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������1���෴���DZ�����������������2�������������С�ڱ���������3������ֵ�������෴�������Ǹ�������4��������������������1����5����![]() ����a=b����6��û�������������������ĸ�����.������ȷ�ĸ����� ��
����a=b����6��û�������������������ĸ�����.������ȷ�ĸ����� ��
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
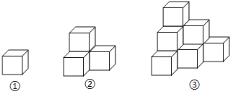
����Ŀ����������ͼ����ı������
���и�ͼ���ⳤΪ![]() ��С������ڳɵģ���ͼ���У�����
��С������ڳɵģ���ͼ���У�����![]() ��С�����壬�����濴��
��С�����壬�����濴��![]() �������Σ������Ϊ
�������Σ������Ϊ![]() ����ͼ���У�����
����ͼ���У�����![]() ��С�����壬�����濴��
��С�����壬�����濴��![]() �������Σ������Ϊ
�������Σ������Ϊ![]() ����ͼ�ۣ�����
����ͼ�ۣ�����![]() ��С�����壬�����濴��
��С�����壬�����濴��![]() �������Σ������Ϊ
�������Σ������Ϊ![]() ����
����
![]() ��
��![]() ��ͼ�У����ж��ٸ�С�����壿�����濴�ж��ٸ������Σ�������Ƕ��٣�
��ͼ�У����ж��ٸ�С�����壿�����濴�ж��ٸ������Σ�������Ƕ��٣�
![]() ��
��![]() ��ͼ���У������濴�ж��ٸ������Σ�������Ƕ��٣�
��ͼ���У������濴�ж��ٸ������Σ�������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com