
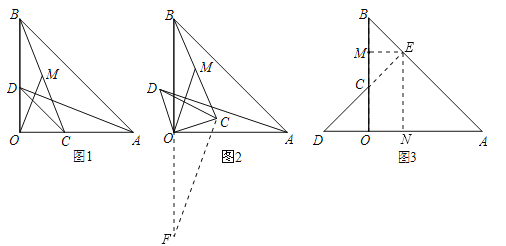
����Ŀ����֪������AOB����COD�У�OA=OB��OC=OD����AOB=��COD=90����
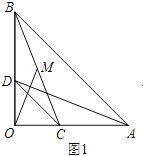
��1����ͼ1����C��D�ֱ��ڱ�OA��OB�ϣ�����AD��BC����MΪ�߶�BC���е㣬����OM���������ж��߶�AD��OM֮���������ϵ,������֤����
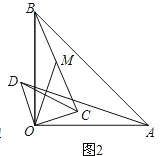
��2����ͼ2����ͼ1�е���COD�Ƶ�O��ʱ����ת����ת��Ϊ����0��������90����������AD��BC����MΪ�߶�BC���е㣬����OM�������жϣ�1���еĽ����Ƿ���Ȼ����������������֤����������������˵�����ɣ�
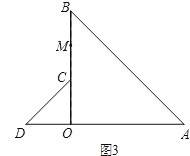
��3����ͼ3����ͼ1�е���COD�Ƶ�O��ʱ����ת��ʹ��COD��һ��ODǡ������AOB�ı�OA��ͬһ��ֱ����ʱ����C����OB�ϣ���MΪ�߶�BC���е㣮�����жϣ�1�����߶�AD��OM֮���������ϵ�Ƿ����仯��д����IJ��룬������֤����
���𰸡���1��OM��![]() �����ɼ���������2�����������ɼ���������3�����仯�����ɼ�����
�����ɼ���������2�����������ɼ���������3�����仯�����ɼ�����
����������������1��AD��OM֮���������ϵΪAD=2OM��
��2����1���еĽ�����Ȼ����������Ϊ����ͼ2��ʾ���ӳ�BO��F��ʹFO=BO������CF����M��O�ֱ�ΪBC��BF���е����õ�OMΪ������BCF����λ����������λ�߶����õ�FC=2OM������SAS�õ�������AOD��������FOCȫ��������ȫ�������εĶ�Ӧ����ȵõ�FC=AD�����������õ�AD=2OM��
��3����1�����߶�AD��OM֮���������ϵû�з����仯������Ϊ����ͼ3��ʾ���ӳ�DC��AB��E������ME������E��EN��AD��N����������COD��������AOB��Ϊ����ֱ�������������õ���ֱ�������ε����ʵõ��ĸ���Ϊ45���������õ�������MCE��������AEDΪ����ֱ��������������ENΪֱ��������ADEб���ϵ����ߵõ�AD=2EN��������������Ϊֱ�ǵ��ı���Ϊ���εõ��ı���OMENΪ�������ɵó�EN=OM�����������õ�AD=2OM��
�������1���߶�AD��OM֮���������ϵ��AD=2OM��
��2����1���Ľ�����Ȼ����������Ϊ��
֤������ͼ2���ӳ�BO��F��ʹFO=BO������CF��
��MΪBC�е���OΪBF�е�����MOΪ��BCF����λ������FC=2OM��
�ߡ�AOB=��AOF=��COD=90�㣬���AOB+��BOD=��AOF+��AOC������AOD=��FOC������AOD�͡�FOC���� 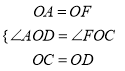 �����AOD�ա�FOC��SAS������FC=AD����AD=2OM��
�����AOD�ա�FOC��SAS������FC=AD����AD=2OM��
��3����1�����߶�AD��OM֮���������ϵû�з����仯������Ϊ��
֤������ͼ3���ӳ�DC��AB��E������ME������E��EN��AD��N��
��OA=OB��OC=OD����AOB=��COD=90�㣬���A=��D=��B=��BCE=��DCO=45�㣬��AE=DE��BE=CE����AED=90�㣬��DN=AN����AD=2NE��
��MΪBC���е�����EM��BC�����ı���ONEM�Ǿ�������NE=OM����AD=2OM��
�ʴ�Ϊ��AD=2OM��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
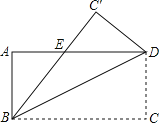
����Ŀ����ͼ������ABCD����ֱ��BD�۵���ʹ��C����C������BC����AD�ڵ�E��AD=8��AB=6����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
��������ͬ����������һ��͵õ�һ�����������ǰ�����Ϊ���������������磺234234��3939���ȣ����������������У�234234��Ϊ��λ��������3939��Ϊ��λ��������
��1����д��һ����λ�������� �������� ������ܡ����ܡ�����13������
��2���Ƿ�������λ�����������ܱ�13��������˵�����ɣ�
��3����һ����λ��������ΪM�����ĸ�λ����֮�͵�3����ΪN��M��N�Ľ���ܱ�13��������������λ�������м�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������������������ij������ʱ���Ը߳�����20%��ۣ���֪����۵ľ��������������9���뽫���ֱ��0.2��Ԫ����4��������ͬ��
��1����ÿ������Ľ��ۺͱ�۷ֱ��Ƕ�����Ԫ��
��2�����ÿ������Ľ��۲��䣬����1��������ı�۳��ۣ��õ�ƽ��ÿ�¿��۳��������20������ÿ������ÿ����0.1��Ԫ����ÿ�¿ɶ��۳�2������ÿ��������۶�����Ԫ����ÿ�»��������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ8��B��������λ�ڵ�A���һ�㣬��AB=20��
��1��д�������ϵ�B��ʾ������ ����
��2��|5��3|��ʾ5��3֮��ľ���ֵ��ʵ����Ҳ������Ϊ5��3���������������Ե�����֮��ľ��룮��|x��3|�ļ��������������ϱ�ʾ������x�ĵ����ʾ������3�ĵ�֮��ľ��룮��̽����
�٣���|x��8|=2����x=�� ����
����|x+12|+|x��8|����СֵΪ�� ����
��3������P��O���������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮��tΪ������ʱ��A��P����֮��ľ���Ϊ2��
��4������P��Q�ֱ��O��B���㣬ͬʱ��������P��ÿ��5����λ�������������������˶���Q����P���ٶȵ����������������������˶������˶�ʱ��Ϊt��t��0���룮�ʵ�tΪ������ʱ��P��Q֮��ľ���Ϊ4��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������㣻��������������![]() ��
��![]() ������
������![]() ����ʽ�ұ���ͨ���ļӷ����������˷����㣬���磬����
����ʽ�ұ���ͨ���ļӷ����������˷����㣬���磬����![]() ��
��![]() �ڸ��������½��Ϊ
�ڸ��������½��Ϊ![]() ���������£�
���������£�
![]()
![]() ��
��![]() ��ֵ��
��ֵ��
![]() ����������
����������![]() ��
��![]() �������¶���һ����������
�������¶���һ����������![]() ����ʹ������
����ʹ������![]() ��
��![]() ���㶨���������������Ľ��Ϊ
���㶨���������������Ľ��Ϊ![]() ��д���㶨���������________��
��д���㶨���������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD��BC��E��CD���е㣬����AE���ӳ���BC���ӳ����ڵ�F����AB��AE����AB=5��AE=6�����������µ�֮��Ϊ �� 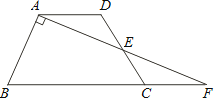
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ���������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺
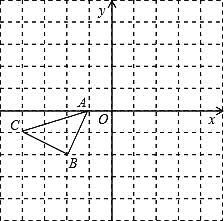
��1����A��Ϊ��ת���ģ�����ABC�Ƶ�A˳ʱ����ת90������AB1C1��������AB1C1��
��2��������ABC��������ԭ��O�����ĶԳƵ���A2B2C2��
��3��������C����x��ĶԳƵ�P������P����ƽ��x��xȡ����������λ���Ⱥ�������A2B2C2���ڲ�����ֱ��д��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c����A���� ![]() ��0����B��3
��0����B��3 ![]() ��0����C��0��3�����㣬�߶�BC�������ߵĶԳ����ཻ��D���������ߵĶ���ΪP������PA��AD��DP���߶�AD��y���ཻ�ڵ�E��
��0����C��0��3�����㣬�߶�BC�������ߵĶԳ����ཻ��D���������ߵĶ���ΪP������PA��AD��DP���߶�AD��y���ཻ�ڵ�E�� 
��1����������ߵĽ���ʽ��
��2����ƽ��ֱ������ϵ���Ƿ���ڵ�Q��ʹ��Q��C��DΪ��������������ADPȫ�ȣ������ڣ������Q�����ꣻ�������ڣ�˵�����ɣ�
��3������CED�Ƶ�E˳ʱ����ת����EC��ת�����߶�BC�ཻ�ڵ�M����ED��ת����Գ����ཻ�ڵ�N������PM��DN����PM=2DN�����N�����ֱ꣨��д���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com