
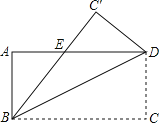
【题目】如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=6,求AE的长。
【答案】AE的长为![]() .
.
【解析】试题分析:先根据折叠的性质得到∠DBC=∠DBE,再由AD∥BC得到∠DBC=∠BDE,则∠DBE=∠BDE,于是可判断BE=DE设AE=x,则DE=BE=8-x,然后在Rt△ABE中利用勾股定理得到x2+62=(8-x)2,再解方程即可.
试题解析:∵矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,
∴∠C′BD=∠CBD,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠CBD,
∴∠EDB=∠C′BD,
∴EB=ED,
设AE=x,则ED=AD﹣AE=8﹣x,BE=8﹣x,
在Rt△ABE中,
∵AB2+AE2=BE2,
∴62+x2=(8﹣x)2,解得x=![]() ,
,
即AE的长为![]() 。
。


科目:初中数学 来源: 题型:
【题目】某工程队(有甲、乙两组)承接了世界园艺博览会的一项小型工程任务,这项任务规定在若干天内完成.已知甲组单独完成这项工程所需时间比规定时间多20天,乙组单独完成这项工程所需时间比规定时间多10天.如果甲、乙两组先合作15天,剩下的由甲单独做,则正好如期完成,那么规定的时间是多少天?(列方程解应用题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3交y轴于点C,直线l为抛物线的对称轴,点P在第三象限且为抛物线的顶点.P到x轴的距离为 ![]() ,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B.
,到y轴的距离为1.点C关于直线l的对称点为A,连接AC交直线l于B. 
(1)求抛物线的表达式;
(2)直线y= ![]() x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y=
x+m与抛物线在第一象限内交于点D,与y轴交于点F,连接BD交y轴于点E,且DE:BE=4:1.求直线y= ![]() x+m的表达式;
x+m的表达式;
(3)若N为平面直角坐标系内的点,在直线y= ![]() x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
x+m上是否存在点M,使得以点O、F、M、N为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.
(1)若BF=BD=![]() ,求BE的长;
,求BE的长;
(2)若∠ADE=2∠BFE,求证:FH=HE+HD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点B、E、C、F在一条直线上,AB = DF,AC = DE,BE = CF.
求证: (1) △ABC ≌ △DFE ;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】决心试一试,请阅读下列材料:计算:![]()
解法一:原式=![]()
=![]()
=![]()
解法二:原式=![]()
=![]()
=![]()
=![]()
解法三:原式的倒数为:![]()
=![]()
=﹣20+3﹣5+12
=﹣10
故原式 =![]()
上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的,在正确的解法中,你认为解法 最简捷.然后请解答下列问题,计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A、B两款汽车,已知A款汽车每辆进价为![]() 万元,B款汽车每辆进价为6万元.
万元,B款汽车每辆进价为6万元.
![]() 公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?
公司预计用不多于135万元且不少于129万元的资金购进这两款汽车共20辆,有几种进货方案,它们分别是什么?
![]() 如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使
如果A款汽车每辆售价为9万元,B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使![]() 中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
中所有的方案获利相同,a值应是多少,此种方案是什么?(提示:可设购进B款汽车x辆)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
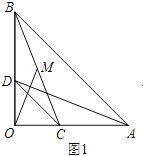
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则请你判断线段AD与OM之间的数量关系,并加以证明.
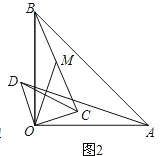
(2)如图2,将图1中的△COD绕点O逆时针旋转,旋转角为α(0°<α<90°).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
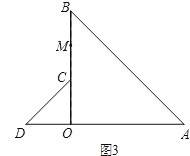
(3)如图3,将图1中的△COD绕点O逆时针旋转到使△COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com