
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯy=ax2+bx+cҫӯ№эAЈЁ©Ғ ![]() Ј¬0Ј©ЎўBЈЁ3
Ј¬0Ј©ЎўBЈЁ3 ![]() Ј¬0Ј©ЎўCЈЁ0Ј¬3Ј©ИэөгЈ¬ПЯ¶ОBCУлЕЧОпПЯөД¶ФіЖЦбПаҪ»УЪDЈ®ёГЕЧОпПЯөД¶ҘөгОӘPЈ¬Б¬ҪУPAЎўADЎўDPЈ¬ПЯ¶ОADУлyЦбПаҪ»УЪөгEЈ®
Ј¬0Ј©ЎўCЈЁ0Ј¬3Ј©ИэөгЈ¬ПЯ¶ОBCУлЕЧОпПЯөД¶ФіЖЦбПаҪ»УЪDЈ®ёГЕЧОпПЯөД¶ҘөгОӘPЈ¬Б¬ҪУPAЎўADЎўDPЈ¬ПЯ¶ОADУлyЦбПаҪ»УЪөгEЈ® 
ЈЁ1Ј©ЗуёГЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ФЪЖҪГжЦұҪЗЧшұкПөЦРКЗ·сҙжФЪөгQЈ¬К№ТФQЎўCЎўDОӘ¶ҘөгөДИэҪЗРОУлЎчADPИ«өИЈҝИфҙжФЪЈ¬ЗуіцөгQөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ»
ЈЁ3Ј©Ҫ«ЎПCEDИЖөгEЛіКұХлРэЧӘЈ¬ұЯECРэЧӘәуУлПЯ¶ОBCПаҪ»УЪөгMЈ¬ұЯEDРэЧӘәуУл¶ФіЖЦбПаҪ»УЪөгNЈ¬Б¬ҪУPMЎўDNЈ¬ИфPM=2DNЈ¬ЗуөгNөДЧшұкЈЁЦұҪУРҙіцҪб№ыЈ©Ј®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©
ҪвЈәЙиЕЧОпПЯөДҪвОцКҪОӘЈәy=aЈЁx+ ![]() Ј©ЈЁx©Ғ3
Ј©ЈЁx©Ғ3 ![]() Ј©Ј¬ҙъИлөгCЈЁ0Ј¬3Ј©әуЈ¬өГЈә
Ј©Ј¬ҙъИлөгCЈЁ0Ј¬3Ј©әуЈ¬өГЈә
aЈЁ0+ ![]() Ј©ЈЁ0©Ғ3
Ј©ЈЁ0©Ғ3 ![]() Ј©=3Ј¬ҪвөГ a=©Ғ
Ј©=3Ј¬ҪвөГ a=©Ғ ![]()
ЎаЕЧОпПЯөДҪвОцКҪЈәy=©Ғ ![]() ЈЁx+
ЈЁx+ ![]() Ј©ЈЁx©Ғ3
Ј©ЈЁx©Ғ3 ![]() Ј©=©Ғ
Ј©=©Ғ ![]() x2+
x2+ ![]() x+3
x+3
ЈЁ2Ј©
ҪвЈәЙиЦұПЯBCөДҪвОцКҪЈәy=kx+bЈ¬ТАМвТвЈ¬УРЈә
![]() Ј¬
Ј¬
ҪвөГ 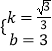 Ј®
Ј®
№КЦұПЯBCЈәy=©Ғ ![]() x+3Ј®
x+3Ј®
УЙЕЧОпПЯөДҪвОцКҪЦӘЈәPЈЁ ![]() Ј¬4Ј©Ј¬Ҫ«өгPөДәбЧшұкҙъИлЦұПЯBCЦРЈ¬өГЈәDЈЁ
Ј¬4Ј©Ј¬Ҫ«өгPөДәбЧшұкҙъИлЦұПЯBCЦРЈ¬өГЈәDЈЁ ![]() Ј¬2Ј©Ј®
Ј¬2Ј©Ј®
ЙиөгQЈЁxЈ¬yЈ©Ј¬ФтУРЈә
QC2=ЈЁx©Ғ0Ј©2+ЈЁy©Ғ3Ј©2=x2+y2©Ғ6y+9ЎўQD2=ЈЁx©Ғ ![]() Ј©2+ЈЁy©Ғ2Ј©2=x2+y2©Ғ2
Ј©2+ЈЁy©Ғ2Ј©2=x2+y2©Ғ2 ![]() x©Ғ4y+7Ј»
x©Ғ4y+7Ј»
¶шЈәPA2=ЈЁ©Ғ ![]() ©Ғ
©Ғ ![]() Ј©2+ЈЁ0©Ғ4Ј©2=28ЎўAD2=ЈЁ©Ғ
Ј©2+ЈЁ0©Ғ4Ј©2=28ЎўAD2=ЈЁ©Ғ ![]() ©Ғ
©Ғ ![]() Ј©2+ЈЁ0©Ғ2Ј©2=16ЎўCD=PD=2Ј»
Ј©2+ЈЁ0©Ғ2Ј©2=16ЎўCD=PD=2Ј»
ЎчQCDәНЎчAPDЦРЈ¬CD=PDЈ¬ИфБҪёцИэҪЗРОИ«өИЈ¬ФтЈә
ўЩQC=APЎўQD=ADКұЈ¬ ![]()
ўЪQC=ADЎўQD=APКұЈ¬ ![]()
ҪвўЩЎўўЪөД·ҪіМЧйЈ¬өГЈә ![]() Ўў
Ўў ![]() Ўў
Ўў ![]() Ўў
Ўў ![]() Ј»
Ј»
ЎаөгQөДЧшұкОӘЈЁ3 ![]() Ј¬4Ј©ЎўЈЁ
Ј¬4Ј©ЎўЈЁ ![]() Ј¬©Ғ2Ј©ЎўЈЁ©Ғ2
Ј¬©Ғ2Ј©ЎўЈЁ©Ғ2 ![]() Ј¬1Ј©»тЈЁ0Ј¬7Ј©
Ј¬1Ј©»тЈЁ0Ј¬7Ј©
ЈЁ3Ј©
ҪвЈәёщҫЭМвТвЧчНјИзУТНјЈ»

УЙDЈЁ ![]() Ј¬2Ј©ЎўBЈЁ3
Ј¬2Ј©ЎўBЈЁ3 ![]() Ј¬0Ј©ЦӘЈәDF=2Ј¬BF=2
Ј¬0Ј©ЦӘЈәDF=2Ј¬BF=2 ![]() Ј»
Ј»
ЎаЎПBDF=ЎПADF=ЎПCDE=ЎПDCE=60ЎгЈ¬јҙЎчCEDКЗөИұЯИэҪЗРОЈ»
ФЪЎчCEMәНЎчDENЦРЈ¬ 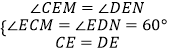
ЎаЎчCEMЎХЎчDENЈ¬Фт CM=DNЈ¬PM=2CM=2DNЈ»
ЙиөгMЈЁxЈ¬©Ғ ![]() x+3Ј©Ј¬ФтУРЈә
x+3Ј©Ј¬ФтУРЈә
PM2=ЈЁ ![]() ©ҒxЈ©2+ЈЁ4+
©ҒxЈ©2+ЈЁ4+ ![]() x©Ғ3Ј©2=
x©Ғ3Ј©2= ![]() x2©Ғ
x2©Ғ ![]()
![]() x+4ЎўCM2=x2+
x+4ЎўCM2=x2+ ![]() x2=
x2= ![]() x2Ј»
x2Ј»
ТСЦӘЈәPM2=4CM2Ј¬ФтУРЈә
![]() x2©Ғ
x2©Ғ ![]()
![]() x+4=4ЎБ
x+4=4ЎБ ![]() x2Ј¬ҪвөГ x=
x2Ј¬ҪвөГ x= ![]() Ј»
Ј»
ЎаCM=DN= ![]() ЎБx=
ЎБx= ![]() ЎБ
ЎБ ![]() =
= ![]() Ј»
Ј»
ФтЈәFN=DF©ҒDN=2©Ғ ![]() =
= ![]() Ј¬
Ј¬
ЎаөгNЈЁ ![]() Ј¬
Ј¬ ![]() Ј©Ј®
Ј©Ј®
ЎҫҪвОцЎҝЈЁ1Ј©ТСЦӘЕЧОпПЯҫӯ№эөДИэөгЧшұкЈ¬ЦұҪУАыУГҙэ¶ЁПөКэ·ЁЗуҪвјҙҝЙЈ®ЈЁ2Ј©УЙУЪөгQөДО»ЦГҝЙДЬУРЛДҙҰЈ¬ЛщТФАыУГјёәО·ЁЗуҪвҪПОӘёҙФУЈ¬ЛщТФҝЙҝјВЗЦұҪУУГSSSЕР¶ЁБҪИэҪЗРОИ«өИөД·Ҫ·ЁАҙЗуҪвЈ®ДЗГҙЈ¬КЧПИТӘЦӨГчCD=DPЈ¬ЙиіцөгQөДЧшұкәуЈ¬ұнКҫіцQCЎўQDөДіӨЈ¬И»әуУЙБнБҪЧй¶ФУҰұЯПаөИБР·ҪіМАҙИ·¶ЁөгQөДЧшұкЈ®ЈЁ3Ј©ёщҫЭBЎўDөДЧшұкЈ¬ИЭТЧЕР¶ПіцЎчCDEКЗөИұЯИэҪЗРОЈ¬И»әуНЁ№эЦӨЎчCEMЎўЎчDENИ«өИАҙөГіцCM=DNЈ¬КЧПИЙиіцөгMөДЧшұкЈ¬ұнКҫіцPMЎўCMөДіӨЈ¬УЙPM=2DN=2CMБР·ҪіМИ·¶ЁөгMөДЧшұкЈ¬ҪшТ»ІҪөГөҪCMөДіӨәуЈ¬јҙҝЙөГіцDNөДіӨЈ¬УЙҙЛЗуөГөгNөДЧшұкЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
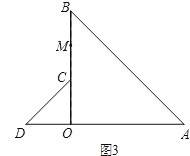
ЎҫМвДҝЎҝТСЦӘЈәФЪЎчAOBУлЎчCODЦРЈ¬OA=OBЈ¬OC=ODЈ¬ЎПAOB=ЎПCOD=90ЎгЈ®
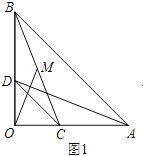
ЈЁ1Ј©ИзНј1Ј¬өгCЎўD·ЦұрФЪұЯOAЎўOBЙПЈ¬Б¬ҪбADЎўBCЈ¬өгMОӘПЯ¶ОBCөДЦРөгЈ¬Б¬ҪбOMЈ¬ФтЗлДгЕР¶ППЯ¶ОADУлOMЦ®јдөДКэБҝ№ШПө,ІўјУТФЦӨГчЈ®
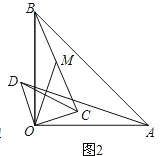
ЈЁ2Ј©ИзНј2Ј¬Ҫ«Нј1ЦРөДЎчCODИЖөгOДжКұХлРэЧӘЈ¬РэЧӘҪЗОӘҰБЈЁ0ЎгЈјҰБЈј90ЎгЈ©Ј®Б¬ҪбADЎўBCЈ¬өгMОӘПЯ¶ОBCөДЦРөгЈ¬Б¬ҪбOMЈ®ЗлДгЕР¶ПЈЁ1Ј©ЦРөДҪбВЫКЗ·сИФИ»іЙБўЈ®ИфіЙБўЈ¬ЗлЦӨГчЈ»ИфІ»іЙБўЈ¬ЗлЛөГчАнУЙЈ»
ЈЁ3Ј©ИзНј3Ј¬Ҫ«Нј1ЦРөДЎчCODИЖөгOДжКұХлРэЧӘөҪК№ЎчCODөДТ»ұЯODЗЎәГУлЎчAOBөДұЯOAФЪН¬Т»МхЦұПЯЙПКұЈ¬өгCВдФЪOBЙПЈ¬өгMОӘПЯ¶ОBCөДЦРөгЈ®ЗлДгЕР¶ПЈЁ1Ј©ЦРПЯ¶ОADУлOMЦ®јдөДКэБҝ№ШПөКЗ·с·ўЙъұд»ҜЈ¬РҙіцДгөДІВПлЈ¬ІўјУТФЦӨГчЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Т»МхЕЧОпПЯУлxЦбПаҪ»УЪAЎўBБҪөгЈ¬Жд¶ҘөгPФЪХЫПЯC©ҒD©ҒEЙПТЖ¶ҜЈ¬ИфөгCЎўDЎўEөДЧшұк·ЦұрОӘЈЁ©Ғ1Ј¬4Ј©ЎўЈЁ3Ј¬4Ј©ЎўЈЁ3Ј¬1Ј©Ј¬өгBөДәбЧшұкөДЧоРЎЦөОӘ1Ј¬ФтөгAөДәбЧшұкөДЧоҙуЦөОӘЈЁ Ј©
A.1
B.2
C.3
D.4
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
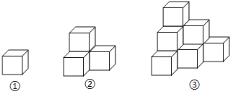
ЎҫМвДҝЎҝёщҫЭИэКУНјЗујёәОМеөДұнГж»эЈ®
ПВБРёчНјКЗАвіӨОӘ![]() өДРЎХэ·ҪМе°ЪіЙөДЈ¬ИзНјўЩЦРЈ¬№ІУР
өДРЎХэ·ҪМе°ЪіЙөДЈ¬ИзНјўЩЦРЈ¬№ІУР![]() ёцРЎХэ·ҪМеЈ¬ҙУХэГжҝҙУР
ёцРЎХэ·ҪМеЈ¬ҙУХэГжҝҙУР![]() ёцХэ·ҪРОЈ¬ұнГж»эОӘ
ёцХэ·ҪРОЈ¬ұнГж»эОӘ![]() Ј»ИзНјўЪЦРЈ¬№ІУР
Ј»ИзНјўЪЦРЈ¬№ІУР![]() ёцРЎХэ·ҪМеЈ¬ҙУХэГжҝҙУР
ёцРЎХэ·ҪМеЈ¬ҙУХэГжҝҙУР![]() ёцХэ·ҪРОЈ¬ұнГж»эОӘ
ёцХэ·ҪРОЈ¬ұнГж»эОӘ![]() Ј»ИзНјўЫЈ¬№ІУР
Ј»ИзНјўЫЈ¬№ІУР![]() ёцРЎХэ·ҪМеЈ¬ҙУХэГжҝҙУР
ёцРЎХэ·ҪМеЈ¬ҙУХэГжҝҙУР![]() ёцХэ·ҪРОЈ¬ұнГж»эОӘ
ёцХэ·ҪРОЈ¬ұнГж»эОӘ![]() Ј»Ўӯ
Ј»Ўӯ
![]() өЪ
өЪ![]() ёцНјЦРЈ¬№ІУР¶аЙЩёцРЎХэ·ҪМеЈҝҙУХэГжҝҙУР¶аЙЩёцХэ·ҪРОЈҝұнГж»эКЗ¶аЙЩЈҝ
ёцНјЦРЈ¬№ІУР¶аЙЩёцРЎХэ·ҪМеЈҝҙУХэГжҝҙУР¶аЙЩёцХэ·ҪРОЈҝұнГж»эКЗ¶аЙЩЈҝ
![]() өЪ
өЪ![]() ёцНјРОЦРЈ¬ҙУХэГжҝҙУР¶аЙЩёцХэ·ҪРОЈҝұнГж»эКЗ¶аЙЩЈҝ
ёцНјРОЦРЈ¬ҙУХэГжҝҙУР¶аЙЩёцХэ·ҪРОЈҝұнГж»эКЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј,Хэ·ҪРОABCDЦР,AB=6,өгEФЪұЯCDЙП,ЗТCD=3DE.Ҫ«ЎчADEСШAE¶ФХЫЦБЎчAFE,СУіӨEFҪ»ұЯBCУЪөгG,Б¬ҪбAGЎўCF.ПВБРҪбВЫЦРХэИ·ҪбВЫөДёцКэКЗ ( )

ўЩЎчABGЎХЎчAFGЈ»ўЪЎПEAG=450Ј»ўЫBG=GCЈ» ўЬAGЎОCFЈ» ўЭSЎчFGC=3.6
A. 2ёц B. 3ёц C. 4ёц D. 5ёц
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»БҫЖыіөФЪұКЦұөД№«В·ЙПРРК»,БҪҙО№ХНдәу,ИФФЪФӯАҙөД·ҪПтЙПЖҪРРЗ°Ҫш,ДЗГҙХвБҪҙО№ХНдөДҪЗ¶ИКЗЈЁ Ј©
A. өЪТ»ҙОПтУТ№Х40, өЪ¶юҙОПтЧу№Х140
B. өЪТ»ҙОПтЧу№Х40, өЪ¶юҙОПтУТ№Х40
C. өЪТ»ҙОПтЧу№Х40, өЪ¶юҙОПтЧу№Х140
D. өЪТ»ҙОПтУТ№Х40, өЪ¶юҙОПтУТ№Х40Ўг
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФД¶БАнҪвЈәТ»ХЕҫШРОЦҪЖ¬Ј¬јфПВТ»ёцХэ·ҪРОЈ¬КЈПВТ»ёцҫШРОЈ¬іЖОӘөЪТ»ҙОІЩЧчЈ»ФЪКЈПВөДҫШРОЦҪЖ¬ЦРФЩјфПВТ»ёцХэ·ҪРОЈ¬КЈПВТ»ёцҫШРОЈ¬іЖОӘөЪ¶юҙОІЩЧчЈ»ЎӯЈ»ИфФЪөЪnҙОІЩЧчәуЈ¬КЈПВөДҫШРООӘХэ·ҪРОЈ¬ФтіЖФӯҫШРООӘnҪЧЖжТмҫШРОЈ®ИзНј1Ј¬ҫШРОABCDЦРЈ¬ИфAB=3Ј¬BC=9Ј¬ФтіЖҫШРОABCDОӘ2ҪЧЖжТмҫШРОЈ®
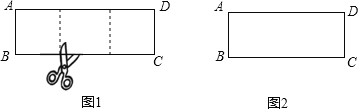
ЈЁ1Ј©ЕР¶ПУлІЩЧчЈә
ИзНј2Ј¬ҫШРОABCDіӨОӘ7Ј¬ҝнОӘ3Ј¬ЛьКЗЖжТмҫШРОВрЈҝИз№ыКЗЈ¬ЗлРҙіцЛьКЗјёҪЧЖжТмҫШРОЈ¬ІўФЪНјЦР»ӯіцІГјфПЯЈ»Из№ыІ»КЗЈ¬ЗлЛөГчАнУЙЈ®
ЈЁ2Ј©МҪҫҝУлјЖЛгЈә
ТСЦӘҫШРОABCDөДТ»ұЯіӨОӘ20Ј¬БнТ»ұЯіӨОӘaЈЁaЈј20Ј©Ј¬ЗТЛьКЗ3ҪЧЖжТмҫШРОЈ¬Зл»ӯіцҫШРОABCDј°ІГјфПЯөДКҫТвНјЈ¬ІўФЪНјөДПВ·ҪРҙіцaөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈәИзНјЈ¬ФЪЖҪРРЛДұЯРОABCDЦРЈ¬OОӘ¶ФҪЗПЯBDөДЦРөгЈ¬№эөгOөДЦұПЯEF·ЦұрҪ»ADЈ¬BCУЪEЈ¬FБҪөгЈ¬Б¬ҪбBEЈ¬DFЈ®
ЈЁ1Ј©ЗуЦӨЈәЎчDOEЎХЎчBOFЈ®
ЈЁ2Ј©өұЎПDOEөИУЪ¶аЙЩ¶ИКұЈ¬ЛДұЯРОBFDEОӘБвРОЈҝЗлЛөГчАнУЙЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
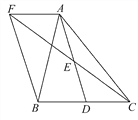
ЎҫМвДҝЎҝИзНј,ФЪЎчABCЦРЈ¬DКЗBCұЯЙПөДТ»өг,EКЗADөДЦРөг,№эAөгЧчBCөДЖҪРРПЯҪ»CEөДСУіӨПЯУЪөгFЈ¬ЗТAF=BD,Б¬ҪУBFЈ®
(1)ЗуЦӨЈәBD=CDЈ»
(2)өұЎчABCВъЧгКІГҙМхјюКұ,ЛДұЯРОAFBDКЗҫШРО?ІўЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com