
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论中正确结论的个数是 ( )

①△ABG≌△AFG;②∠EAG=450;③BG=GC; ④AG∥CF; ⑤S△FGC=3.6
A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】分析:①用HL证明△ABG≌△AFG;②由△ADE≌△AFE,△ABG≌△AFG,得到∠EAG=![]() ∠BAD;③在直角三角形CEG中,由勾股定理求GC的长;④根据基本图形“等腰三角形+角平分线→平行线”证明;⑤由GF:EG=3:5,得S△FCG:S△ECG=3:5.
∠BAD;③在直角三角形CEG中,由勾股定理求GC的长;④根据基本图形“等腰三角形+角平分线→平行线”证明;⑤由GF:EG=3:5,得S△FCG:S△ECG=3:5.
详解:①根据轴对称的性质得,△ADE≌△AFE,
所以AD=AF,∠AFE=∠D=90°.
因为AB=AD,∠B=90°,所以AB=AF,
因为AG=AG,所以△ABG≌△AFG.
则①正确;
②因为△ADE≌△AFE,△ABG≌△AFG,
所以∠DAE=∠FAE,∠BAG=∠FAG,
所以∠EAG=∠FAE+∠FAE=![]() ∠BAD=
∠BAD=![]() ×90°=45°.
×90°=45°.
则②正确;
③因为△ADE≌△AFE,△ABG≌△AFG,
所以ED=EF,GB=GF,所以EG=DE+BG,
设BG=x,则CG=FG=6-x,DE=2,CE=4,EG=x+2=x+2.
Rt△CEG中,由勾股定理得,CG2+CE2=EG2,
所以(6-x)2+42=(x+2)2,解得x=3.
则CG=6-x=3,又BG=x=3,所以BG=CG.
则③正确;
④因为△ABG≌△AFG,所以∠AGB=∠AGF.
因为BG=CG,BG=GF,所以CG=GF,所以∠GCF=∠GFC.
因为∠BGE=∠GCF+∠GFC,所以∠AGB=∠GCF,所以AG∥CF.
则④正确;
⑤因为GF=3,GE=5,所以S△FGC=![]() S△GCE=
S△GCE=![]() ×GC·CE=
×GC·CE=![]() ×
×![]() ×3×4=3.6.
×3×4=3.6.
则⑤正确.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段BD、CE交于点M.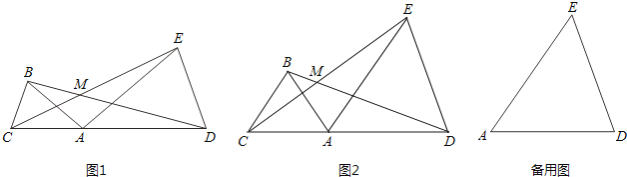
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB=BC=kAC,AD=ED=kAE,则线段BD与CE的数量关系为 , ∠BMC=(用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接EC并延长交BD于点M.则∠BMC=(用α表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象都经过点A(﹣2,6)和点(4,n).
的图象都经过点A(﹣2,6)和点(4,n).
(1)求这两个函数的解析式;
(2)直接写出不等式kx+b≤ ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:一粒米微不足道,平时在饭桌上总会毫不经意地掉下几粒,甚至有些挑食的同学把整碗米饭倒掉.针对这种浪费粮食现象,老师组织同学们进行了实际测算,称得![]() 粒大米约重
粒大米约重![]() 克.
克.
尝试解决:
![]() 粒米重约多少克?
粒米重约多少克?
![]() 按我国现有人口
按我国现有人口![]() 亿,每年
亿,每年![]() 天,每人每天三餐计算,若每人每餐节约
天,每人每天三餐计算,若每人每餐节约![]() 粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)
粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)
![]() 假设我们把一年节约的大米卖成钱,按每千克
假设我们把一年节约的大米卖成钱,按每千克![]() 元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到
元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣ ![]() ,0)、B(3
,0)、B(3 ![]() ,0)、C(0,3)三点,线段BC与抛物线的对称轴相交于D.该抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E.
,0)、C(0,3)三点,线段BC与抛物线的对称轴相交于D.该抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E. 
(1)求该抛物线的解析式;
(2)在平面直角坐标系中是否存在点Q,使以Q、C、D为顶点的三角形与△ADP全等?若存在,求出点Q的坐标;若不存在,说明理由;
(3)将∠CED绕点E顺时针旋转,边EC旋转后与线段BC相交于点M,边ED旋转后与对称轴相交于点N,连接PM、DN,若PM=2DN,求点N的坐标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= ![]() 的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
的图象上,若点A的坐标为(﹣2,﹣3),则k的值为( )
A.1
B.﹣5
C.4
D.1或﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:有理数xA用数轴上点A表示,xA叫做点A在数轴上的坐标;有理数xB用数轴上点B表示,xB叫做点B在数轴上的坐标.|AB|表示数轴上的两点A,B之间的距离.
(1)借助数轴,完成下表:
xA | xB | xA﹣xB | |AB| |
3 | 2 | 1 | 1 |
1 | 5 |
|
|
2 | ﹣3 |
|
|
﹣4 | 1 |
|
|
﹣5 | ﹣2 |
|
|
﹣3 | ﹣6 |
|
|
(2)观察(1)中的表格内容,猜想|AB|= ;(用含xA,xB的式子表示,不用说理)
(3)已知点A在数轴上的坐标是﹣2,且|AB|=8,利用(2)中的结论求点B在数轴上的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了更好地活跃校园文化生活,拟对本校自办的“辉煌”校报进行改版.先从全校学生中随机抽取一部分学生进行了一次问卷调查,题目为“你最喜爱校报的哪一个板块”(每人只限选一项).问卷收集整理后绘制了不完整的频数分布表和如图扇形统计图.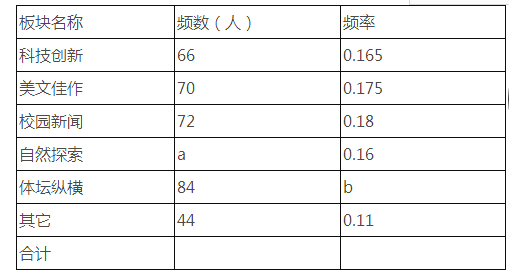
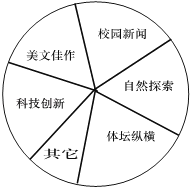
(1)填空:频数分布表中a= , b=;
(2)“自然探索”板块在扇形统计图中所占的圆心角的度数为;
(3)在参加此次问卷调查的学生中,最喜爱哪一个板块的人数最多?有多少人喜欢?
(4)若全校有1500人,估计喜欢“校园新闻”板块的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com