
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
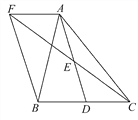
【答案】(1)证明见解析(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
【解析】分析:(1)由AF与BC平行,利用两直线平行内错角相等得到一对角相等,再一对对顶角相等,且由E为AD的中点,得到AE=DE,利用AAS得到△AFE与△DCE全等,利用全等三角形的对应边相等即可得证;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形,理由为:由AF与BD平行且相等,得到四边形AFBD为平行四边形,再由AB=AC,BD=CD,利用三线合一得到AD垂直于BC,即∠ADB为直角,即可得证.
详解:(1)∵AF∥BC,
∴∠AFE=∠DCE.
∵E是AD的中点,
∴AE=DE .
在△AEF和△DEC中,
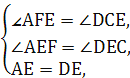
∴△AEF≌△DEC(AAS),
∴AF=CD.
∵AF=BD,
∴BD=CD.
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过A(﹣ ![]() ,0)、B(3
,0)、B(3 ![]() ,0)、C(0,3)三点,线段BC与抛物线的对称轴相交于D.该抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E.
,0)、C(0,3)三点,线段BC与抛物线的对称轴相交于D.该抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E. 
(1)求该抛物线的解析式;
(2)在平面直角坐标系中是否存在点Q,使以Q、C、D为顶点的三角形与△ADP全等?若存在,求出点Q的坐标;若不存在,说明理由;
(3)将∠CED绕点E顺时针旋转,边EC旋转后与线段BC相交于点M,边ED旋转后与对称轴相交于点N,连接PM、DN,若PM=2DN,求点N的坐标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
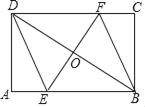
【题目】如图,在矩形ABCD中,AB=8,BC=4,过对角线BD的中点O的直线分别交AB、CD于点E、F,连接DE,BF.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-2)+(-3)+5
(2)![]() ×5÷
×5÷![]() ×5
×5
(3)12-7×(-4)+8÷(-2)
(4)-14+(2-5)2-2
(5)2÷(-2)+0÷7-(-8)×(-2)
(6)(-1)5×(-5)÷[(-3)2+2×(-5)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了更好地活跃校园文化生活,拟对本校自办的“辉煌”校报进行改版.先从全校学生中随机抽取一部分学生进行了一次问卷调查,题目为“你最喜爱校报的哪一个板块”(每人只限选一项).问卷收集整理后绘制了不完整的频数分布表和如图扇形统计图.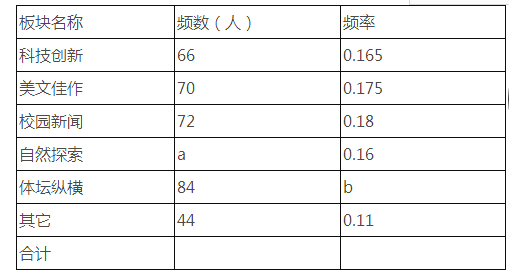
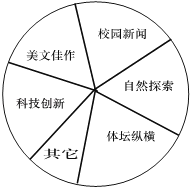
(1)填空:频数分布表中a= , b=;
(2)“自然探索”板块在扇形统计图中所占的圆心角的度数为;
(3)在参加此次问卷调查的学生中,最喜爱哪一个板块的人数最多?有多少人喜欢?
(4)若全校有1500人,估计喜欢“校园新闻”板块的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,灯的质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利润21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表所示:
等级(x级) | 一级 | 二级 | 三级 | … |
生产量(y台/天) | 78 | 76 | 74 | … |
(1)已知护眼灯每天的生产量y(台)是等级x(级)的一次函数,请直接写出y与x之间的函数关系式:;
(2)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是( )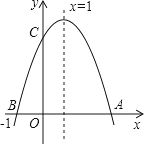
A.①④
B.①③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆放假时,小明一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆。早上从家里出发,向东走了6千米到超市买东西,然后又向东走了1.5千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里。
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)问超市A和外公家C相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家所经历路程小车的耗油量。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月29日,国家发改委批复了昌景黄铁路项目可行性研究报告.该项目位于赣皖两省,线路起自江西省南昌市南昌东站,经上饶市、景德镇市,安徽省黄山市,终至黄山北站.按照设计,行驶180千米,昌景黄高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少20分钟,求昌景黄高铁列车的平均行驶速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com