
【题目】如图,在梯形ABCD中,AD∥BC,E是CD的中点,连接AE并延长交BC的延长线于点F,且AB⊥AE.若AB=5,AE=6,则梯形上下底之和为 . 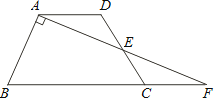
【答案】13
【解析】解:∵在梯形ABCD中,AD∥BC,
∴∠F=∠DAE,∠ECF=∠D,
∵E是CD的中点,
∴DE=CE,
在△ADE和△FCE中, ,
,
∴△ADE≌△FCE(AAS),
∴CF=AD,EF=AE=6,
∴AF=AE+EF=12,
∵AB⊥AE,
∴∠BAF=90°,
∵AB=5,
∴BF= ![]() =13,
=13,
∴AD+BC=BC+CF=BF=13.
所以答案是:13.
【考点精析】关于本题考查的勾股定理的概念和梯形的定义,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形才能得出正确答案.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,距小明家楼下D点20米的B处有一根废弃的电线杆AB,经测得此电线杆与水平线DB所成锐角为60°,在小明家楼顶C处测得电线杆顶端A的俯角为30°,底部点B的俯角为45°(点A、B、D、C在同一平面内).已知在以点B为圆心,10米长为半径的圆形区域外是一休闲广场,有关部门想把此电线杆水平放倒,且B点不动,为安全起见,他们想知道这根电线杆放倒后,顶端A能否落在休闲广场内?请通过计算回答.
(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)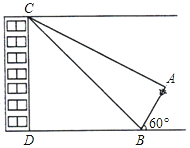
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
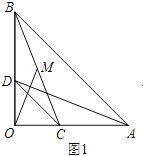
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则请你判断线段AD与OM之间的数量关系,并加以证明.
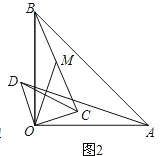
(2)如图2,将图1中的△COD绕点O逆时针旋转,旋转角为α(0°<α<90°).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
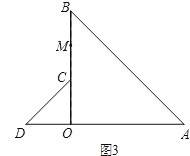
(3)如图3,将图1中的△COD绕点O逆时针旋转到使△COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的周长为24cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于( ) 
A.3cm
B.4cm
C.2.5cm
D.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若![]() ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A(体操)、B(乒乓球)、C(毽球)、D(跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图。
请根据统计图回答下列问题:
(1)这次被调查的学生共有_____人;
(2)请将统计图2补充完整;
(3)统计图1中B项目对应的扇形的圆心角是 _____度;
(4)已知该校共有学生1000人,根据调查结果估计该校喜欢体操的学生有_____人.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
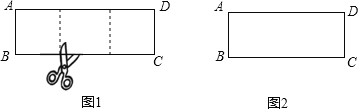
【题目】阅读理解:一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=3,BC=9,则称矩形ABCD为2阶奇异矩形.
(1)判断与操作:
如图2,矩形ABCD长为7,宽为3,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com