
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
已知⊙O的半径为2,点P是⊙O内一点,且OP=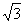 ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A发,以每秒5个单位长度的速度沿数轴向左匀速运动,设时间为t(t>0)秒.
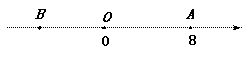
(1)写出数轴上点B表示的数_________,点P表示的数_____________(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x-8|是否有最小值?如果有,直接写出最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线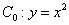 ,顶点记作
,顶点记作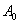 .首先我们将抛物线
.首先我们将抛物线 关于直线
关于直线 对称翻折过去得到抛物线
对称翻折过去得到抛物线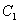 称为第一次操作,再将抛物线
称为第一次操作,再将抛物线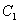 关于直线
关于直线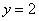 对称翻折过去得到抛物线
对称翻折过去得到抛物线 称为第二次操作,…,将抛物线
称为第二次操作,…,将抛物线 关于直线
关于直线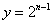 对称翻折过去得到抛物线
对称翻折过去得到抛物线 (顶点记作
(顶点记作 )称为第n此操作(n=1,2,3…),….设抛物线
)称为第n此操作(n=1,2,3…),….设抛物线 与抛物线
与抛物线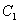 交于两点
交于两点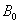 与
与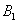 ,顺次连接
,顺次连接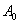 、
、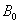 、
、 、
、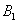 四个点得到四边形
四个点得到四边形 ,抛物线
,抛物线 与抛物线
与抛物线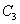 交于两点
交于两点 与
与 ,顺次连接
,顺次连接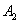 、
、 、
、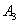 、
、 四个点得到四边形
四个点得到四边形 ,…,抛物线
,…,抛物线 与抛物线
与抛物线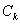 交于两点
交于两点 与
与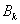 ,顺次连接
,顺次连接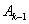 、
、 、
、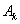 、
、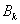 四个点得到四边形
四个点得到四边形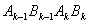 (k=1,3,5…),….
(k=1,3,5…),….
(1)请分别直接写出抛物线 (n=1,2,3,4)的解析式;
(n=1,2,3,4)的解析式;
 (2)一系列四边形
(2)一系列四边形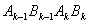 (k=1,3,5…)
(k=1,3,5…)
为哪种特殊的四边形(说明理由)?它们
都相似吗?如果全都相似,请证明之;如
果不全都相似,请举出一对不相似的反例;
(3)试归纳出抛物线 的解析式,无需证明.
的解析式,无需证明.
并利用你归纳出来的 的解析式
的解析式
求四边形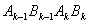 (k=1,3,5…)
(k=1,3,5…)
的面积(用含k的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com