
分析 (1)直接利用完全平方公式得出(x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$)2=x+x-1+2,进而得出答案;
(2)直接利用完全平方公式得出(x+x-1)2=x2+2+x-2,进而得出答案;
(3)直接利用完全平方公式得出x4+x-4=47,进而得出答案.
解答 解:(1)∵x+x-1=3,
∴(x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$)2=x+x-1+2=5,
∴x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$=$\sqrt{5}$;
(2)∵x+x-1=3,
∴(x+x-1)2=x2+2+x-2=9,
∴x2+x-2=7;
(3)∵x2+x-2=7,
∴(x2+x-2)2=49,
∴x4+x-4=47,
∴(x2-x-2)2=x4+x-4-2=45,
∴x2-x-2=±3$\sqrt{5}$.
点评 此题主要考查了完全平方公式的应用,熟练应用完全平方公式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
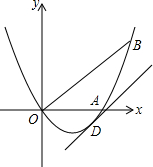 如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,东西和南北街道交于点O,甲沿东西道由西向东走,速度是每秒4m,乙沿南北道由南向北走,速度是每秒3m,当乙通过O点后又继续前进50m时,甲刚好通过O点,当甲、乙相距85m时,求每个人的位置.
如图所示,东西和南北街道交于点O,甲沿东西道由西向东走,速度是每秒4m,乙沿南北道由南向北走,速度是每秒3m,当乙通过O点后又继续前进50m时,甲刚好通过O点,当甲、乙相距85m时,求每个人的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com