
| A. | y2>y3>y1 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
分析 根据反比例函数图象上点的坐标特征得到-$\frac{1}{2}$•y1=-1,-$\frac{1}{4}$•y2=-1,$\frac{1}{2}$•y3=-1,然后解方程求出y1,y2,y3,再比较它们的大小.
解答 解:根据题意得-$\frac{1}{2}$•y1=-1,-$\frac{1}{4}$•y2=-1,$\frac{1}{2}$•y3=-1,解得y1=2,y2=4,y3=-2,
所以y3<y1<y2.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
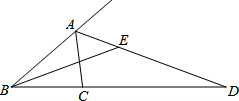 在△ABC中,∠ACB=2∠B,AD为△ABC的外角平分线交射线BC于点D,作∠ABC的角平分线交AD于点E.若CD=5,AC=2,则tan∠AEB=$\frac{\sqrt{3}}{3}$.
在△ABC中,∠ACB=2∠B,AD为△ABC的外角平分线交射线BC于点D,作∠ABC的角平分线交AD于点E.若CD=5,AC=2,则tan∠AEB=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
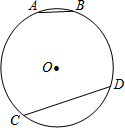 如图,在半径为R的⊙O中,$\widehat{AB}$和$\widehat{CD}$度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).( )
如图,在半径为R的⊙O中,$\widehat{AB}$和$\widehat{CD}$度数分别为36°和108°,弦CD与弦AB长度的差为(用含有R的代数式表示).( )| A. | R | B. | $\frac{1}{2}R$ | C. | 2R | D. | 3R |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第几天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 销售(元/千克) | 400 | A | 250 | 240 | 200 | 150 | 125 | 120 |
| 销售量(千克) | 30 | 40 | 48 | B | 60 | 80 | 96 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 27 | B. | 12 | C. | 18 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
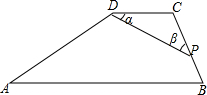 如图,四边形ABCD中,AB∥CD,P为BC上一点,设∠CDP=∠α,∠CPD=∠β,当P在BC上移动时,总有∠α+∠β=∠B成立?请你利用你学过的数学知识说明理由.
如图,四边形ABCD中,AB∥CD,P为BC上一点,设∠CDP=∠α,∠CPD=∠β,当P在BC上移动时,总有∠α+∠β=∠B成立?请你利用你学过的数学知识说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com