
分析 (1)先约分,直接得结果;
(2)先确定积的符号,是负数,然后倍数和倍数相乘,作为二次根式的倍数,被开方数与被开方数相乘,最后要化成最简二次根式;
(3)与(2)同理,要注意a与b的取值.
解答 解:(1)$\frac{2\sqrt{{x}^{2}y}}{3\sqrt{xy}}$=$\frac{2\sqrt{xy}•\sqrt{x}}{3\sqrt{xy}}$=$\frac{2\sqrt{x}}{3}$;
(2)$\sqrt{1\frac{3}{5}}$•2$\sqrt{3}$•(-$\frac{1}{2}$$\sqrt{10}$),
=-2×$\frac{1}{2}$$\sqrt{\frac{8}{5}×3×10}$,
=-$\sqrt{16×3}$,
=-4$\sqrt{3}$;
(3)3a$\sqrt{12ab}$•(-$\frac{2}{3}$$\sqrt{2b}$)(a>0,b>0),
=-3a•$\frac{2}{3}$$\sqrt{24a{b}^{2}}$,
=-2a•$\sqrt{4{b}^{2}•6a}$,
=-4ab$\sqrt{6a}$.
点评 本题是二次根式的乘除混合运算,先确定其符号,再将倍数相乘除,作为结果的倍数,再把被开方数相乘除,结果要化成最简二次根式;要注意能约分的要先约分再化简.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
 如图,在公路l两旁的点A,B处各有一个村庄,为了方便村民们乘车,公交公司决定在公路边建一个公交停靠站,请你通过作图确定公交停靠站P的位置,使得A、B两处的村民到公交站P的距离相等(保留作图痕迹,简要写出作法).
如图,在公路l两旁的点A,B处各有一个村庄,为了方便村民们乘车,公交公司决定在公路边建一个公交停靠站,请你通过作图确定公交停靠站P的位置,使得A、B两处的村民到公交站P的距离相等(保留作图痕迹,简要写出作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数y=$\frac{16}{x}$在第一象限内的图象经过点A,与BC交于点F,OB=3$\sqrt{3}$,BF=$\frac{1}{2}$BC.过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO,若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标.
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数y=$\frac{16}{x}$在第一象限内的图象经过点A,与BC交于点F,OB=3$\sqrt{3}$,BF=$\frac{1}{2}$BC.过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO,若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
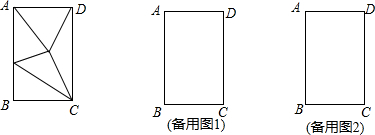
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com