Question

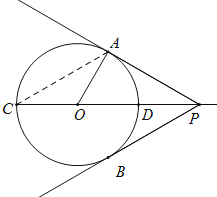
【题目】如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线PA，PB，切点分别为点A，B．

（1）连接AC，若∠APO=30°，试证明△ACP是等腰三角形；

（2）填空：

①当DP= cm时，四边形AOBD是菱形；

②当DP= cm时，四边形AOBP是正方形．

Answer 1

【答案】（1）证明见解析；（2）1；-1．

【解析】

试题分析：（1）利用切线的性质可得OC⊥PC．利用同弧所对的圆周角等于圆心角的一半，求得∠ACP=30°，从而求得．

（2）①要使四边形AOBD是菱形，则OA=AD=OD，所以∠AOP=60°，所以OP=2OA，DP=OD．

②要使四边形AOBP是正方形，则必须∠AOP=45°，OA=PA=1，则OP=，所以DP=OP-1．

试题解析：（1）连接OA，AC

∵PA是⊙O的切线，

∴OA⊥PA，

在Rt△AOP中，∠AOP=90°-∠APO=90°-30°=60°，

∴∠ACP=30°，

∵∠APO=30°

∴∠ACP=∠APO，

∴AC=AP，

∴△ACP是等腰三角形．

（2）①DP=1，理由如下：

∵四边形AOBD是菱形，

∴OA=AD=OD，

∴∠AOP=60°，

∴OP=2OA，DP=OD．

∴DP=1，

②DP=-1，理由如下：

∵四边形AOBP是正方形，

∴∠AOP=45°，

∵OA=PA=1，OP=，

∴DP=OP-1

∴DP=-1．