
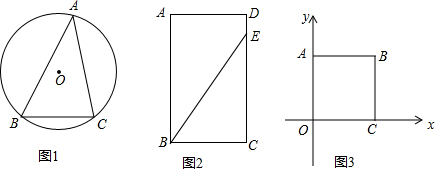
分析 (1)连接OB、OC,只要证明△OBC是等边三角形即可.
(2)如图2中,作BC的垂直平分线,交BE于点O,以O为圆心,OB为半径作圆,交垂直平分线于点P,则点P为所求.
(3)如图3中,在x轴上方作△OKC,使得△OKC是以OC为斜边的等腰直角三角形,作KE⊥AB于E.当EK=KC=时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+$\sqrt{2}$,在AB上只有一个点P满足∠OPC=$\frac{1}{2}$OKC=45°,当BK=$\sqrt{2}$时,在AB上恰好有两个点P满足∠OPC=$\frac{1}{2}$∠OKC=45°,此时m=BC=2,由此不难得出结论.
解答 解:(1)如图1中,连接OB、OC.
∵∠BOC=2∠A,∠A=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=2,
故答案为:2;
(2)如图2中,作BC的垂直平分线,交BE于点O;
以O为圆心,OB为半径作圆,交垂直平分线于点P,
则点P为所求.
(3)如图3中,在x轴上方作△OKC,使得△OKC是以OC为斜边的等腰直角三角形,作KE⊥AB于E.
∵OC=2,
∴OK=KC=$\sqrt{2}$,
当EK=KC=$\sqrt{2}$时,以K为圆心,KC为半径的圆与AB相切,此时m=BC=1+$\sqrt{2}$,在AB上只有一个点P满足∠OPC=$\frac{1}{2}$∠OKC=45°,
当BK=$\sqrt{2}$时,在AB上恰好有两个点P满足∠OPC=$\frac{1}{2}$∠OKC=45°,此时m=BC=2,
综上所述,满足条件的m的值的范围为2≤m<1+$\sqrt{2}$.
故答案为2≤m<1+$\sqrt{2}$.
点评 本题考查圆综合题、圆周角定理、作图-复杂作图、勾股定理、等腰直角三角形的性质等知识,解题的关键是灵活应用圆周角等于同弧所对的圆心角的一半解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图:在平面直角坐标系xOy中,直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A、B两点,P是直线AB上一动点,⊙P的半径为1.
已知如图:在平面直角坐标系xOy中,直线y=$\sqrt{3}$x-2$\sqrt{3}$与x轴、y轴分别交于A、B两点,P是直线AB上一动点,⊙P的半径为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com