
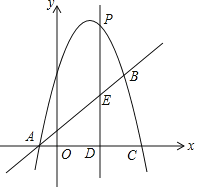
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P是抛物线上的一个动点
点P是抛物线上的一个动点![]() 不与点A、点B重合
不与点A、点B重合![]() ,过点P作直线
,过点P作直线![]() 轴于点D,交直线AB于点E.
轴于点D,交直线AB于点E.
![]() 当
当![]() 时,求P点坐标;
时,求P点坐标;
![]() 是否存在点P使
是否存在点P使![]() 为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)点P坐标为
(2)点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】分析:(1)由直线解析式可求得B点坐标,由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)①可设出P点坐标,则可表示出E、D的坐标,从而可表示出PE和ED的长,由条件可知到关于P点坐标的方程,则可求得P点坐标;②由E、B、C三点坐标可表示出BE、CE和BC的长,由等腰三角形的性质可得到关于E点坐标的方程,可求得E点坐标,则可求得P点坐标.
详解:![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
把A、B、C三点坐标代入抛物线解析式可得 ,解得
,解得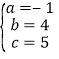 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,P与A重合不合题意,舍去,
时,P与A重合不合题意,舍去,
![]() ;
;
当![]() 时,解得
时,解得![]() 或
或![]() ,但当
,但当![]() 时,P与A重合不合题意,舍去,
时,P与A重合不合题意,舍去,
![]() ;
;
综上可知P点坐标为![]() 或
或![]() ;
;
![]() 设
设![]() ,则
,则![]() ,且
,且![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
当![]() 为等腰三角形时,则有
为等腰三角形时,则有![]() 、
、![]() 或
或![]() 三种情况,
三种情况,
当![]() 时,则
时,则![]() ,解得
,解得![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
当![]() 时,则
时,则![]() ,解得
,解得![]() 或
或![]() ,此时P点坐标为
,此时P点坐标为![]() 或
或![]() ;
;
当![]() 时,则
时,则![]() ,解得
,解得![]() 或
或![]() ,当
,当![]() 时E点与B点重合,不合题意,舍去,此时P点坐标为
时E点与B点重合,不合题意,舍去,此时P点坐标为![]() ;
;
综上可知存在满足条件的点P,其坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着人民生活水平不断提高,家庭轿车的拥有量逐年增加,据统计,某小区16年底拥有家庭轿车640辆,到18年底家庭轿车拥有量达到了1000辆.
(1)若该小区家庭轿车的年平均增长量都相同, 请求出这个增长率;
(2)为了缓解停车矛盾,该小区计划投入15万元用于再建若干个停车位,若室内每个车位0.4万元,露天车位每个0.1万元,考虑到实际因素,计划露天车位数量大于室内车位数量的2倍,但小于室内数量的3.5倍,求出所有可能的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
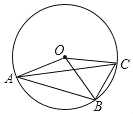
【题目】如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是( )个.
①AB=2BC;②![]() =2
=2![]() ;③∠ACB=2∠CAB;④∠ACB=∠BOC.
;③∠ACB=2∠CAB;④∠ACB=∠BOC.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
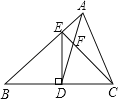
(1)求证:△ABC~△FCD;
(2)若△DEF的面积为2,求△FCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
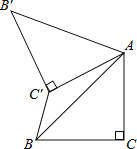
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.
,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.
(1)求∠ABC'的度数;
(2)求C'B的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
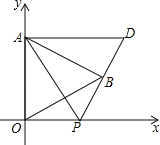
【题目】如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.求:DP的长及点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com