
【题目】如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是( )个.
①AB=2BC;②![]() =2
=2![]() ;③∠ACB=2∠CAB;④∠ACB=∠BOC.
;③∠ACB=2∠CAB;④∠ACB=∠BOC.
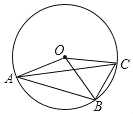
A.1B.2C.3D.4
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给![]() 人.
人.
(1)求第一轮后患病的人数;(用含![]() 的代数式表示)
的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
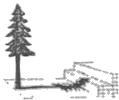
【题目】在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得落在教学楼第一级台阶上的影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
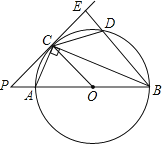
【题目】在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是![]() 上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
(1)求证:∠PCA=∠PBC;
(2)若PC=8,PA=4,∠ECD=∠PCA,以点C为圆心,半径为5作⊙C,试判断⊙C与直线BD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
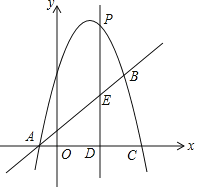
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P是抛物线上的一个动点
点P是抛物线上的一个动点![]() 不与点A、点B重合
不与点A、点B重合![]() ,过点P作直线
,过点P作直线![]() 轴于点D,交直线AB于点E.
轴于点D,交直线AB于点E.
![]() 当
当![]() 时,求P点坐标;
时,求P点坐标;
![]() 是否存在点P使
是否存在点P使![]() 为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
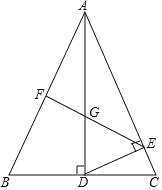
【题目】如图,在△ABC中.AB=AC,AD⊥BC于D,作DE⊥AC于E,F是AB中点,连EF交AD于点G.
(1)求证:AD2=ABAE;
(2)若AB=3,AE=2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com