
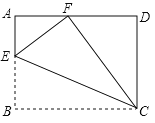
【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=3,BC=4,则tan∠AFE=__.
科目:初中数学 来源: 题型:
【题目】某校在“校园体育文化节”活动中组织了“球类知识我知道”的竞赛活动,从初三年级1200名学生中随机抽查了100名学生的成绩(满分30分),整理得到如下的统计图表:
成绩(分) | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
频率统计表
成绩分组 | 频数 | 频率 |
15≤x<18 | 3 | 0.03 |
18≤x<21 | a | 0.12 |
21≤x<24 | 20 | 0.20 |
24≤x<27 | 35 | 0.35 |
27≤x≤30 | 30 | b |
频数分布直方图
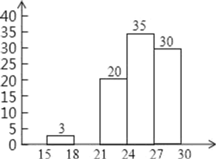
请根据所提供的信息解答下列问题:
(1)样本的众数是 分,中位数是 分;
(2)频率统计表中a= ,b= ;补全频数分布直方图;
(3)请根据抽样统计结果,估计该次竞赛中初三年级成绩不少于21分的大约有多少人?随机抽取一名同学的成绩,其值不小于24分的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间满足关系:
(元)之间满足关系:![]() ,其图像如图所示.
,其图像如图所示.
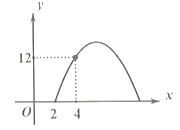
(1)销售单价为多少元时,这种商品每天的销售利润最大?最大利润为多少元?
(2)若该商品每天的销售利润不低于12元,则销售单价![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是( )个.
①AB=2BC;②![]() =2
=2![]() ;③∠ACB=2∠CAB;④∠ACB=∠BOC.
;③∠ACB=2∠CAB;④∠ACB=∠BOC.
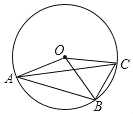
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律:
①该蔬菜的销售价![]() (单位:元/千克)与时间
(单位:元/千克)与时间![]() (单位:月份)满足关系:
(单位:月份)满足关系: ![]() ;
;
②该蔬菜的平均成本![]() (单位:元/千克)与时间
(单位:元/千克)与时间![]() (单位:月份)满足二次函数关系
(单位:月份)满足二次函数关系![]() .已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
.已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润![]() (单位:元/千克)最大?最大平均利润是多少?(注:平均利润
(单位:元/千克)最大?最大平均利润是多少?(注:平均利润![]() 销售价
销售价![]() 平均成本)
平均成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com