
���� ��1���۲��俵Ľⷨ�ҳ������IJ��裬д�������ʽ���ɣ�
��2�������䷽��������̵Ľ⼴�ɣ�
��� �⣺��1����俵Ľⷨ�ӵ��IJ���ʼ���ִ���b2-4ac��0ʱ������ax2+bx+c=0��a��0���������ʽ��x=$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$��
�ʴ�Ϊ���ģ�x=$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$��
��2��x2-2x=24��
�䷽�ã�x2-2x+1=24+1������x-1��2=25��
�����ã�x-1=��5��
��ã�x1=6��x2=-4��
���� ���⿼���˽�һԪ���η���-��ʽ�����䷽�����������ո��ֽⷨ�ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4aǧ�� | B�� | 2aǧ�� | C�� | 200ǧ�� | D�� | 100ǧ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�У���ADC=90�㣬��EΪ��BC�ϵ�һ�㣬����DE����FΪED�ϵ�һ�㣬����AF��BF����AB=AC��AD=AF����BAC=��DAF��
��ͼ���ı���ABCD�У���ADC=90�㣬��EΪ��BC�ϵ�һ�㣬����DE����FΪED�ϵ�һ�㣬����AF��BF����AB=AC��AD=AF����BAC=��DAF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
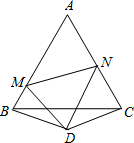 ��ͼ����ABC�DZ߳�Ϊ1�ĵȱ������Σ���BDC�Ƕ��ǡ�BDC=120��ĵ��������Σ���DΪ������һ��60��ǣ��ǵ����߷ֱ�AB��AC��M��N������MN�����AMN���ܳ���
��ͼ����ABC�DZ߳�Ϊ1�ĵȱ������Σ���BDC�Ƕ��ǡ�BDC=120��ĵ��������Σ���DΪ������һ��60��ǣ��ǵ����߷ֱ�AB��AC��M��N������MN�����AMN���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��֪a=b����a2=b2 | B�� | ��֪a=b��mΪ��������������ma=mb | ||
| C�� | ��֪ma=mb��mΪ��������������a=b | D�� | ��֪ax=b����a��0����x=$\frac{b}{a}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com