
 顶角为36°的等腰三角形被叫做“黄金三角形”,如图所示,△ABC为顶角为36°等腰三角形.BD为∠ABC的平分线,过点D作BC的平行线交AB于点E
顶角为36°的等腰三角形被叫做“黄金三角形”,如图所示,△ABC为顶角为36°等腰三角形.BD为∠ABC的平分线,过点D作BC的平行线交AB于点E 分析 (1)根据三角形内角和定理及外角的性质可求出图中所有角的度数,运用等角对等边判定三角形的形状即可;
(2))设BC=x,则BD=AD=x,CD=AB-x,根据(1)得出△ABC∽△BCD,再根据相似的性质得出AB=$\frac{1+\sqrt{5}}{2}$x,从而得出答案.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=(180°-36°)÷2=72°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵DE∥BC,
∴∠DBC=∠BDE=36°,∠AED=∠ABC,∠ADE=∠ACB,
∴∠A=∠ABD,
∠BDE=∠ABD=72°,
∴∠ABC=∠ACB,
∴AD=BD,BE=ED,AE=AD,
∴△ABD、△BDE、△AED是等腰三角形;
∵∠BDC=2∠A=72°,
∴∠BDC=∠BCD,
∴△BCD是等腰三角形,
∴图中等腰三角形有:△ABC,△ABD,△BDE,△AED,△BCD,共5个;
(2)设BC=x,则BD=AD=x,CD=AB-x,
∵△ABC∽△BCD,
∴$\frac{AB}{BC}$=$\frac{BC}{CD}$,
∴$\frac{AB}{x}$=$\frac{x}{AB-x}$,
∴AB=$\frac{1+\sqrt{5}}{2}$x或AB=$\frac{1-\sqrt{5}}{2}$x(舍去),
∴等腰三角形ABC中,腰AB与底边BC的比值是$\frac{{\sqrt{5}+1}}{2}$;
故答案为:5,$\frac{{\sqrt{5}+1}}{2}$;
点评 此题考查了黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 4.38×104 | B. | 4.38×105 | C. | 43.8×103 | D. | 0.438×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 型 号 | A | B |
| 进价(元/件) | 120 | 100 |
| 售价(元/件) | 135 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
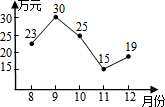 如图是某国产品牌手机专卖店今年8-12月高清大屏手机销售额折线统计图.根据图中信息,可以判断相邻两个月高清大屏手机销售额变化最大的是( )
如图是某国产品牌手机专卖店今年8-12月高清大屏手机销售额折线统计图.根据图中信息,可以判断相邻两个月高清大屏手机销售额变化最大的是( )| A. | 8-9月 | B. | 9-10月 | C. | 10-11月 | D. | 11-12月 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
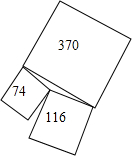 如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?
如图,三个正方形形状的土地面积分别为74英亩,116英亩,370英亩,三个正方形恰好围着一个池塘.现要将这550英亩的土地拍卖,如果有人能计算出池塘的面积,那么池塘不计入土地价钱白白奉送,英国数学家巴尔教授曾经巧妙地解答了这个问题,你能解答吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com