
 △ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC分别交AB、AC于E、F.
△ABC中,∠B与∠C的平分线交于点O,过O作EF∥BC分别交AB、AC于E、F.分析 (1)由BE=EO,根据等边对等角,可得∠EBO=∠EOB,又由△ABC中,∠ABC与∠ACB的平分线交于点O,可得∠EBO=∠OBC,即可判定EF∥BC,则可证得∠FOC=∠OCB=∠OCF,由等角对等边,即可证得OF=CF;
(2)先根据两直线平行内错角相等及角平分线定义,得到∠OBE=∠EOB,根据等角对等边得到EO=BE,同理OF=FC,所以EF=EO+OF=BE+CF.
解答 解:(1)OF=CF.
理由:∵BE=EO,
∴∠EBO=∠EOB,
∵△ABC中,∠ABC与∠ACB的平分线交于点O,
∴∠EBO=∠OBC,
∴∠EOB=∠OBC,
∴EF∥BC,
∴∠FOC=∠OCB=∠OCF,
∴OF=CF;
(2)EF=BE+CF,
∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠OBC=∠EOB,
∴∠EBO=∠EOB;
∴EO=BE,
同理可得OF=FC,
∴EO+OF=BE+FC,
即EF=BE+CF.
点评 本题考查了角平分线定义,平行线的性质,等腰三角形的判定和性质等知识点,关键是推出BE=OE,CF=OF.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,利用一面墙,用长80m的篱笆围成一个矩形场地,能否使所围矩形场地的面积超过800m2?如果能,请求出BC的长,如果不能,请说明理由.
如图,利用一面墙,用长80m的篱笆围成一个矩形场地,能否使所围矩形场地的面积超过800m2?如果能,请求出BC的长,如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
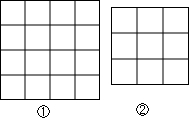 如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是有几个小立方体块搭建成的几何体的俯视图,小正方体中的数字表示在该位置小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.
如图是有几个小立方体块搭建成的几何体的俯视图,小正方体中的数字表示在该位置小立方体块的个数,请画出从正面和从左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB-BA、CD-DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB-BA、CD-DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com