Question

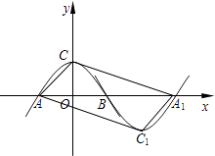
【题目】如图所示，抛物线m：y=ax2+b（a＜0，b＞0）与x轴于点A、B（点A在点B的左侧），与y轴交于点C．将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为C1 ， 与x轴的另一个交点为A1 ．

（1）当a=﹣1，b=1时，求抛物线n的解析式；
（2）四边形AC1A1C是什么特殊四边形，请写出结果并说明理由；
（3）若四边形AC1A1C为矩形，请求出a，b应满足的关系式．

Answer 1

【答案】
（1）

解：当a=﹣1，b=1时，抛物线m的解析式为：y=﹣x2+1．

令x=0，得：y=1．

∴C（0，1）．

令y=0，得：x=±1．

∴A（﹣1，0），B（1，0），

∵C与C1关于点B中心对称，

∴抛物线n的解析式为：y=（x﹣2）2﹣1=x2﹣4x+3

（2）

解：四边形AC1A1C是平行四边形．

理由：连接AC，AC1，A1C1，

∵C与C1、A与A1都关于点B中心对称，

∴AB=BA1，BC=BC1，

∴四边形AC1A1C是平行四边形

（3）

解：令x=0，得：y=b．

∴C（0，b）．

令y=0，得：ax2+b=0，

∴ ，

∴ ，

∴ ．

要使平行四边形AC1A1C是矩形，必须满足AB=BC，

∴ ，

∴ ，

∴ab=﹣3．

∴a，b应满足关系式ab=﹣3．

【解析】（1）根据a=﹣1，b=1得出抛物线m的解析式，再利用C与C1关于点B中心对称，得出二次函数的顶点坐标，即可得出答案；（2）利用两组对边分别相等的四边形是平行四边形即可证明；（3）利用矩形性质得出要使平行四边形AC1A1C是矩形，必须满足AB=BC，即可求出．
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．