
【题目】已知函数f(x)= ![]() (e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(Ⅱ)若对任意x∈( ![]() ,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
(Ⅲ)设g(x)= ![]() ,Tn=1+2[g(
,Tn=1+2[g( ![]() )+g(
)+g( ![]() )+g(
)+g( ![]() )+…+g(
)+…+g( ![]() )](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有
)](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <M成立?若存在,求M的最小值;若不存在,请说明理由.
<M成立?若存在,求M的最小值;若不存在,请说明理由.
【答案】解:(Ⅰ) 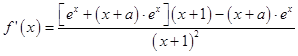 =
= 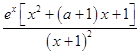 依题意曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直.
依题意曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直.
得: ![]() ,
,
∴a=0,
(Ⅱ)对任意的 ![]() ,(x+1)f(x)≥m(2x﹣1)恒成立.
,(x+1)f(x)≥m(2x﹣1)恒成立.
等价于xex﹣m(2x﹣1)≥0对 ![]() 恒成立,
恒成立,
即 ![]() 对
对 ![]() 恒成立
恒成立
令 ![]() ,则m≤t(x)最小
,则m≤t(x)最小
∵ 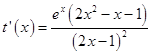
由t′(x)=0得:x=1或 ![]() (舍去)
(舍去)
当 ![]() 时,t′(x)<0;
时,t′(x)<0;
当x∈(1,+∞)时,t′(x)>0
∴t(x)在 ![]() 上递减,在(1,+∞)上递增
上递减,在(1,+∞)上递增
∴t(x)最小=t(1)=e,
∴m≤e.
(Ⅲ) 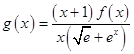 =
= ![]() ,
,![]() ,
,
∴ ![]() ,
,
因此有 ![]()
由 ![]() ,
,![]()
得2Tn=2+2[1+1+…+1]=2+2(n﹣1)=2n,∴Tn=n.![]() ,取n=2m(m∈N*),
,取n=2m(m∈N*),
则 ![]() =
= ![]() =
= ![]() ,
,
当m趋向于+∞时, ![]() 趋向于+∞.
趋向于+∞.
所以,不存在正常数M,对任意给定的正整数n(n≥2),
都有 ![]() 成立
成立
【解析】(Ⅰ)求出导数,利用条件列出方程,即可求实数a的值;(Ⅱ)转化条件为对 ![]() 恒成立,即
恒成立,即 ![]() 对
对 ![]() 恒成立,构造函数
恒成立,构造函数 ![]() ,求出t(x)最小 , 即可得到实数m的取值范围.(Ⅲ)通过
,求出t(x)最小 , 即可得到实数m的取值范围.(Ⅲ)通过 ![]() ,推出
,推出 ![]() ,化简
,化简 ![]() ,推出Tn=n.然后求解
,推出Tn=n.然后求解 ![]() ,取n=2m(m∈N*),利用放缩法推出
,取n=2m(m∈N*),利用放缩法推出 ![]() ≥
≥ ![]() ,当m趋向于+∞时,
,当m趋向于+∞时, ![]() 趋向于+∞.然后说明结果.
趋向于+∞.然后说明结果.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+a.
(1)当a=3时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x﹣3|,x∈R,f(x)+g(x)≥5,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径. (Ⅰ)求直线l的参数方程和圆C的极坐标方程;
,圆C以M为圆心,3为半径. (Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|.
查看答案和解析>>
科目:初中数学 来源: 题型:
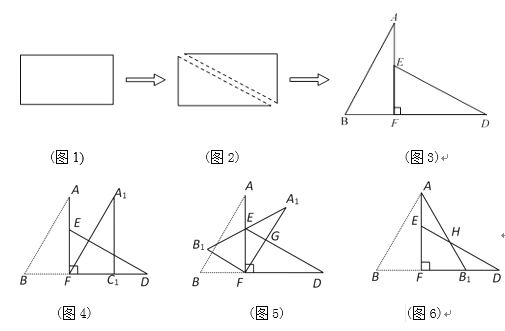
【题目】如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较短直角边长为5cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示),小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆:(x+cosθ)2+(y﹣sinθ)2=1,直线l:y=kx.给出下面四个命题: ①对任意实数k和θ,直线l和圆M有公共点;
②对任意实数k,必存在实数θ,使得直线l和圆M相切;
③对任意实数θ,必存在实数k,使得直线l和圆M相切;
④存在实数k和θ,使得圆M上有一点到直线l的距离为3.
其中正确的命题是(写出所以正确命题的编号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若a∈R,则“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“?x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
D.命题“?x0∈R,使得x02+2x0+3<0”的否定是“?x∈R,x2+2x+3>0”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中x,y∈R,则4x﹣y的最大值为( )
,其中x,y∈R,则4x﹣y的最大值为( ) 
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,且AB∥MN,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M是AD边上距D点最近的n等分点(n≥2,且n为整数),则A′N= . 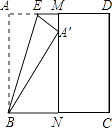
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com