
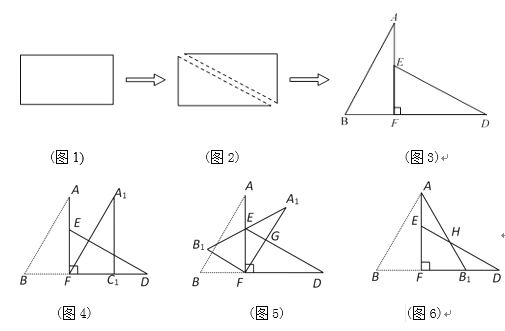
【题目】如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较短直角边长为5cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示),小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH
【答案】(1) 5cm;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据题意,分析可得:图形平移的距离就是线段BF的长,进而在Rt△ABC中求得BF=5cm,即图形平移的距离是5cm;
(2)在Rt△EFD中,求出FD的长,根据直角三角形的性质,可得:FG=![]() FD,即可求得FG的值;
FD,即可求得FG的值;
(3)借助平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,容易证明.
(1)图形平移的距离就是线段BC的长,
∵在Rt△ABC中,斜边长为10cm,∠BAC=30°,
∴BC=5cm,
∴平移的距离为5cm.
(2)∵∠![]() FA=30°,
FA=30°,
∴∠![]() ,∠D=30°.
,∠D=30°.
∴∠![]() .
.
在Rt![]() EFD中,ED=10 cm,
EFD中,ED=10 cm,
∵FD=![]() ,
,
∴![]() cm.
cm.
(3)△AHE与△![]() 中,∵
中,∵![]() ,
,
∵FD=FA,所以EF=FB=FB1,∴![]() ,即AE=D
,即AE=D![]() .
.
又∵![]() ,
,
∴△![]() ≌△
≌△![]() (AAS),
(AAS),
∴![]()


科目:初中数学 来源: 题型:
【题目】已知抛物线E:y2=4x的准线为l,焦点为F,O为坐标原点.
(1)求过点O,F,且与l相切的圆的方程;
(2)过F的直线交抛物线E于A,B两点,A关于x轴的对称点为A′,求证:直线A′B过定点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f(x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 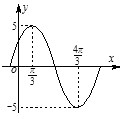
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆 ![]() 内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足
内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足 ![]() (其中λ>0,且λ≠1),若λ变化时,AB的斜率总为
(其中λ>0,且λ≠1),若λ变化时,AB的斜率总为 ![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据某市地产数据研究院的数据显示,2016年该市新建住宅销售均价走势如图所示,为抑制房价过快上涨,政府从8月份采取宏观调控措施,10月份开始房价得到很好的抑制. 
(Ⅰ)地产数据研究院研究发现,3月至7月的各月均价y(万元/平方米)与月份x之间具有较强的线性相关关系,试建立y关于x的回归方程(系数精确到0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
(Ⅱ)地产数据研究院在2016年的12个月份中,随机抽取三个月份的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为X,求X的分布列和数学期望.
参考数据: ![]() =25,
=25, ![]() =5.36,
=5.36, ![]() =0.64
=0.64
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知f(x)=x2(1nx﹣a)+a,则下列结论中错误的是( )
A.a>0,x>0,f(x)≥0
B.a>0,x>0,f(x)≤0
C.a>0,x>0,f(x)≥0
D.a>0,x>0,f(x)≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(Ⅱ)若对任意x∈( ![]() ,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
(Ⅲ)设g(x)= ![]() ,Tn=1+2[g(
,Tn=1+2[g( ![]() )+g(
)+g( ![]() )+g(
)+g( ![]() )+…+g(
)+…+g( ![]() )](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有
)](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <M成立?若存在,求M的最小值;若不存在,请说明理由.
<M成立?若存在,求M的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数列{an}中,a1=4,an>0,前n项和为Sn , 若 ![]() .
.
(1)求数列{an}的通项公式;
(2)若数列 ![]() 的前n项和为Tn , 求Tn .
的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=4 ![]() ,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( ) 
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4 ![]()
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com