
【题目】已知f(x)=x2(1nx﹣a)+a,则下列结论中错误的是( )
A.a>0,x>0,f(x)≥0
B.a>0,x>0,f(x)≤0
C.a>0,x>0,f(x)≥0
D.a>0,x>0,f(x)≤0
【答案】C
【解析】解:∵f(x)=x2(1nx﹣a)+a,x>0, ∴f′(x)=x(21nx﹣2a+1),
令f′(x)=0,解得x= ![]() ,
,
当x∈(0, ![]() )时,f′(x)<0,f(x)单调递减,
)时,f′(x)<0,f(x)单调递减,
当x∈( ![]() ,+∞)时,f′(x)>0,f(x)单调递增,
,+∞)时,f′(x)>0,f(x)单调递增,
当x= ![]() ,函数有最小值,最小值为f(
,函数有最小值,最小值为f( ![]() )=
)= ![]() e2a﹣1+a
e2a﹣1+a
∴f(x)≥f( ![]() )=
)= ![]() e2a﹣1+a,
e2a﹣1+a,
若f(x)≥0恒成立,
只要 ![]() e2a﹣1+a≥0,
e2a﹣1+a≥0,
设g(a)= ![]() e2a﹣1+a,
e2a﹣1+a,
∴g′(a)=1﹣e2a﹣1 ,
令g′(a)=0,解得a= ![]()
当a∈( ![]() ,+∞)时,g′(a)<0,g(a)单调递减,
,+∞)时,g′(a)<0,g(a)单调递减,
当x∈(0, ![]() )时,g′(a)>0,g(a)单调递增
)时,g′(a)>0,g(a)单调递增
∴g(a)<g( ![]() )=0,
)=0,
∴ ![]() e2a﹣1+a≤0,当且仅当a=
e2a﹣1+a≤0,当且仅当a= ![]() 时取等号,存在唯一的实数a=
时取等号,存在唯一的实数a= ![]() ,使得对任意x∈(0,+∞),f(x)≥0,故A,B,D正确,
,使得对任意x∈(0,+∞),f(x)≥0,故A,B,D正确,
当a≠ ![]() 时,f(x)<0,故C错误
时,f(x)<0,故C错误
故选:C
【考点精析】根据题目的已知条件,利用全称命题的相关知识可以得到问题的答案,需要掌握全称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;全称命题的否定是特称命题.
;全称命题的否定是特称命题.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,F1 , F2分别是双曲线 ![]() 的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,
的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1, ![]() ),若△ABF2为等边三角形,则△BF1F2的面积为( )
),若△ABF2为等边三角形,则△BF1F2的面积为( ) 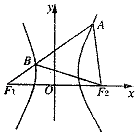
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
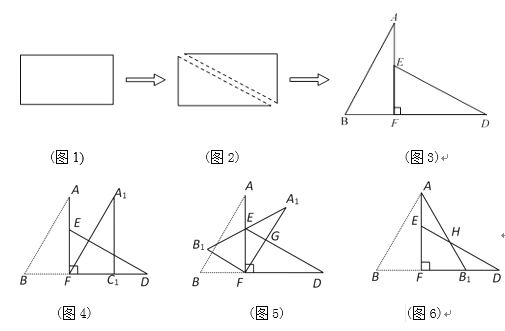
【题目】如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较短直角边长为5cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示),小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD, ![]() .
. 
(1)求证:BC⊥平面ACFE;
(2)点M在线段EF上运动,设平面MAB与平面FCB二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线C由上半椭圆 ![]() 和部分抛物线
和部分抛物线 ![]() 连接而成,C1与C2的公共点为A,B,其中C1的离心率为
连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
.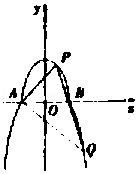
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),是否存在直线l,使得PQ为直径的圆恰好过点A,若存在直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经过市场调查发现,该公司生产的某商品在第x天的销售单价为(x+20)元/件(1≤x≤50),且该商品每天的销量满足关系式y=200﹣4x.已知该商品第10天的售价按8折出售,仍然可以获得20%的利润.
(1)求公司生产该商品每件的成本为多少元?
(2)问销售该商品第几天时,每天的利润最大?最大利润是多少?
(3)该公司每天还需要支付人工、水电和房租等其它费用共计a元,若公司要求每天的最大利润不低于2200元,且保证至少有46天盈利,则a的取值范围是(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com