
【题目】某公司经过市场调查发现,该公司生产的某商品在第x天的销售单价为(x+20)元/件(1≤x≤50),且该商品每天的销量满足关系式y=200﹣4x.已知该商品第10天的售价按8折出售,仍然可以获得20%的利润.
(1)求公司生产该商品每件的成本为多少元?
(2)问销售该商品第几天时,每天的利润最大?最大利润是多少?
(3)该公司每天还需要支付人工、水电和房租等其它费用共计a元,若公司要求每天的最大利润不低于2200元,且保证至少有46天盈利,则a的取值范围是(直接写出结果).
【答案】
(1)解:设该公司生产每件商品的成本为a元,根据题意,
得:0.8×(10+20)﹣a=0.2a,
解得:a=20,
故该公司生产每件商品的成本为20元
(2)解:设第x天的销售利润为W,
则:W=(x+20﹣20)(﹣4x+200)=﹣4x2+200x=﹣4(x﹣25)2+2500,
∴当x=25时,W取得最大值,最大值为2500元,
故问销售该商品第25天时,每天的利润最大,最大利润是2500元
(3)0<a≤300
【解析】解: (3)记公司每天控制人工、水电和房租支出共计a元后利润为P, 则P=﹣4(x﹣25)2+2500﹣a,
根据题意:2500﹣a≥2200,
解得:a≤300,
又∵至少有46天的盈利,
∴﹣4x2+200x﹣a=0的两根x1、x2间距离x1﹣x2≥46,
∴(x1﹣x2)2≥462 , 即(x1+x2)2﹣4x1x2≥462 ,
∵x1+x2=50,x1x2= ![]() ,
,
∴502﹣4× ![]() ≥462 , 解得:a≤384,
≥462 , 解得:a≤384,
综上,0<a≤300,
所以答案是:0<a≤300.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】已知f(x)=x2(1nx﹣a)+a,则下列结论中错误的是( )
A.a>0,x>0,f(x)≥0
B.a>0,x>0,f(x)≤0
C.a>0,x>0,f(x)≥0
D.a>0,x>0,f(x)≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(1,0),且经过点
的右焦点为F(1,0),且经过点 ![]()
(1)求椭圆P的方程;
(2)已知正方形ABCD的顶点A,C在椭圆P上,顶点B,D在直线7x﹣7y+1=0上,求该正方形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y= ![]() (x<0)的图象经过点A.
(x<0)的图象经过点A. 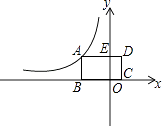
(1)求k值;
(2)把矩形ABCD向左平移,使点C刚好与原点重合,此时线段AB与反比例函数y= ![]() 的交点坐标是什么?
的交点坐标是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=4 ![]() ,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( ) 
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4 ![]()
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB≠BC,连接AC,AE是∠BAD的平分线,交边DC的延长线于点F. 
(1)证明:CE=CF;
(2)若∠B=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.(如图2所示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,QN是⊙O的切线,连接MQ交⊙O于点H,E为![]() 上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
上一点,连接ME,NE,NE交MQ于点F,且ME2=EFEN.
(1)求证:QN=QF;
(2)若点E到弦MH的距离为1,cos∠Q=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从﹣2,﹣1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com