
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为 ![]() ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为 ![]() ,圆C以M为圆心,3为半径. (Ⅰ)求直线l的参数方程和圆C的极坐标方程;
,圆C以M为圆心,3为半径. (Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() .(a为常数,a>0) (Ⅰ)若
.(a为常数,a>0) (Ⅰ)若 ![]() 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;
(Ⅱ)求证:当0<a≤2时,f(x)在 ![]() 上是增函数;
上是增函数;
(Ⅲ)若对任意的a∈(1,2),总存在 ![]() ,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
,使不等式f(x0)>m(1﹣a2)成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f (x)=Asin(ωx+φ),(0<φ<π)的图象如图所示,若f(x0)=3,x0∈( ![]() ,
, ![]() ),则sinx0的值为( )
),则sinx0的值为( ) 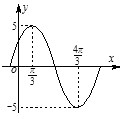
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN= ![]() π,在△ABC中,角A、B、C所对的边分别是a、b、c.
π,在△ABC中,角A、B、C所对的边分别是a、b、c. 
(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;
(Ⅱ)若c= ![]() ,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆 ![]() 内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足
内有一点M(2,1),过M的两条直线l1 , l2分别与椭圆E交于A,C和B,D两点,且满足 ![]() (其中λ>0,且λ≠1),若λ变化时,AB的斜率总为
(其中λ>0,且λ≠1),若λ变化时,AB的斜率总为 ![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据某市地产数据研究院的数据显示,2016年该市新建住宅销售均价走势如图所示,为抑制房价过快上涨,政府从8月份采取宏观调控措施,10月份开始房价得到很好的抑制. 
(Ⅰ)地产数据研究院研究发现,3月至7月的各月均价y(万元/平方米)与月份x之间具有较强的线性相关关系,试建立y关于x的回归方程(系数精确到0.01),政府若不调控,依次相关关系预测第12月份该市新建住宅销售均价;
(Ⅱ)地产数据研究院在2016年的12个月份中,随机抽取三个月份的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为X,求X的分布列和数学期望.
参考数据: ![]() =25,
=25, ![]() =5.36,
=5.36, ![]() =0.64
=0.64
回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(Ⅱ)若对任意x∈( ![]() ,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
(Ⅲ)设g(x)= ![]() ,Tn=1+2[g(
,Tn=1+2[g( ![]() )+g(
)+g( ![]() )+g(
)+g( ![]() )+…+g(
)+…+g( ![]() )](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有
)](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() <M成立?若存在,求M的最小值;若不存在,请说明理由.
<M成立?若存在,求M的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
电量(度) | 电费(元) | |
A | 240 | |
B | ||
合计 | 90 |
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com