
分析 (1)首先求出每个数的平方的大小是多少;然后比较出两个数的平方的大小,即可判断出原来两个数的大小关系.
(2)首先比较出两个数的倒数的大小,然后根据倒数越小,则原来的数越大,判断出原来两个数的大小关系即可.
解答 解:(1)${(\frac{\sqrt{6}}{5})}^{2}$=$\frac{6}{25}$,${(\frac{\sqrt{7}}{6})}^{2}$=$\frac{7}{36}$,
∵$\frac{6}{25}>\frac{7}{36}$,
∴$\frac{\sqrt{6}}{5}$>$\frac{\sqrt{7}}{6}$.
(2)$\frac{1}{\sqrt{15}-\sqrt{14}}=\sqrt{15}+\sqrt{14}$,
$\frac{1}{\sqrt{14}-\sqrt{13}}=\sqrt{14}+\sqrt{13}$,
∵$\sqrt{15}+\sqrt{14}>\sqrt{14}+\sqrt{13}$,
∴$\sqrt{15}$-$\sqrt{14}$<$\sqrt{14}$-$\sqrt{13}$.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
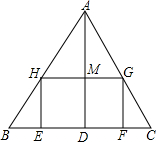 如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.
如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com