练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知，如图，四边形 ABCD，∠A=∠B=Rt∠．

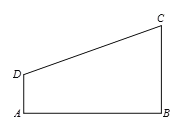
    （1）尺规作图，在线段 AB上找一点 E，使得 EC=ED，连接 EC， ED（不写作法，保留作图痕迹）；

    （2）在（1）在图形中，若∠ADE=∠BEC，且CE=3，BC=，求 AD的长.

    【答案】（1）见解析；（2）2.

    【解析】

    （1）在线段AB上的一点E到C,D的距离相等，即EC=ED，由垂直平分线的性质可知，点E在线段CD的垂直平分线上.

    （2）由勾股定理可求得BE的长；由三角形全等可得AD=BE.

    （1）解：作CD的中垂线交AB于点E.

    （2）解：由(1)知EC=ED，

    又∵∠A=∠B=90°，∠ADE=∠BEC

    ∴△ADE≌△BEC (AAS)，

    ∴AD=BE，

    在Rt△BEC中，

    ∴AD=BE=2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α等于(　　)

    A. 20° B. 30° C. 40° D. 50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

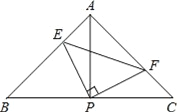
    【题目】如图已知在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB和AC于点E、F，给出以下五个结论正确的个数有（　　）

    ①AE=CF②∠APE=∠CPF ③△BEP≌△AFP④△EPF是等腰直角三角形⑤当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），S四边形AEPF=S△ABC．

    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于x的方程x2-2（m＋1）x＋m2=0.

    （1）当m取何值时，方程有两个实数根？

    （2）为m选取一个合适的整数，使方程有两个不相等的实数根，并求这两个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1摆放矩形纸片ABCD与矩形纸片ECGF，使B、C、G三点在一条直线上，CE在边CD上，连接AF，若M为AF的中点，连接DM、ME.

    (1)试猜想DM与ME的关系，并证明你的结论．

    (2)若将图1中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为______．

    (3)如图2摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的点，则DM和ME的关系为______，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=-2x2,怎样平移这个函数的图象,能使它经过(0,1)和(1,3)两点写出平移后的函数解析式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知抛物线y=-x2+bx+c与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.

    (1)求此抛物线的解析式以及点B的坐标;

    (2)动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M,N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒,当t为何值时,四边形OMPN为矩形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

    （1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；

    （2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？

    （3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58元．如果超市想要每天获得不低于6000元的利润，那么超市每天至少销售粽子多少盒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答下列各题

    （1）解方程：﹣x2+4x﹣3=0．

    （2）已知一次函数y=kx+b的图象与反比例函数y=的图象交于点A（2，m），B（﹣1、n），求一次函数的解析式．

    查看答案和解析>>

    同步练习册答案