
【题目】销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车,用300万元可购进A型轿车10辆,B型轿车15辆;用300万元可购进A型轿车8辆,B型轿车18辆.
(1)求A、B两种型号的轿车每辆分别多少元?
(2)若该汽车销售公司销售一辆A型轿车可获利8000元,销售一辆B型轿车可获利5000元,该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆,且这两种轿车全部售出后总获利不低于20.4万元,问:有几种购车方案?在这几种购车方案中,哪种获利最多?
【答案】
(1)解:设A型轿车每辆x万元,B型轿车每辆y万元.
根据题意,可得 ![]() ,解得:
,解得: ![]() ,
,
15万元=150000元,10万元=100000元.
答:所以A型轿车每辆150000元,B型轿车每辆100000元.
(2)解:设购进A型轿车a辆,则B型轿车(30﹣a)辆.
根据题意,得 ![]() ,解这个不等式组,得18≤a≤20.
,解这个不等式组,得18≤a≤20.
因为a为整数,所以a=18,19,20.
30﹣a的值分别是12,11,10.
因此有三种购车方案:方案一:购进A型轿车18辆,B型轿车12辆;方案二:购进A型轿车19辆,B型轿车11辆;方案三:购进A型轿车20辆,B型轿车10辆.
方案一获利:18×0.8+12×0.5=20.4(万元);
方案二获利:19×0.8+11×0.5=20.7(万元);
方案三获利:20×0.8+10×0.5=21(万元).
【解析】(1)等量关系为:10辆A型轿车总价钱+15辆B型轿车总价钱=300;8辆A型轿车总价钱+18辆B型轿车总价钱=300,把相关数值代入计算即可;(2)关系式为:A型轿车总价钱+B型轿车总价钱≤400;A型轿车总利润+B型轿车总利润≥20.4,求合适的正整数解即可.
【考点精析】根据题目的已知条件,利用一元一次不等式组的应用的相关知识可以得到问题的答案,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1 . (图中每个小方格边长均为1个单位长度).
(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.A1;B1;C1;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示)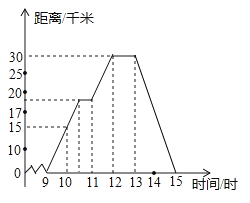
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
(1)报名参加课外活动小组的学生共有 人,将条形图补充完整;

(2)扇形图中m= ,n= ;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,DE垂直平分AC , DF⊥BC , 当△ABC满足条件时,四边形DECF是正方形.(要求:①不再添加任何辅助线,②只需填一个符合要求的条件)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按一定规律排列且形式相似的一列数: 第1个数:a1= ![]() ﹣(1+
﹣(1+ ![]() );
);
第2个数:a2= ![]() ﹣(1+
﹣(1+ ![]() )[1+
)[1+ ![]() ][1+
][1+ ![]() ]
]
第3个数:a3= ![]() ﹣(1+
﹣(1+ ![]() )[1+
)[1+ ![]() ][1+
][1+ ![]() ][1+
][1+ ![]() [1+
[1+ ![]() ]
]
(1)计算这三个数的结果(直接写答案): a1=;a2=;a3=;
(2)请按上述规律写出第4个数a4的形式并计算结果;
(3)请根据上述规律写出第n (n为正整数)个数an的形式(中间部分用省略号,两端部分必须写详细),然后直接写出计算结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com