
��֪����C��A��D��ͬһ��ֱ���ϣ���ABC=��ADE=�����߶�BD��CE���ڵ�M��
��1����ͼ1����AB=AC��AD=AE
�����߶�BD��CE��������������ϵ����˵�����ɣ�
�����BMC�Ĵ�С���æ���ʾ����
��2����ͼ2����AB=BC=kAC��AD=ED=kAE�����߶�BD��CE��������ϵΪ_________����BMC=_________���æ���ʾ����
��3���ڣ�2���������£��ѡ�ABC�Ƶ�A��ʱ����ת180�㣬�ڱ���ͼ��������ת���ͼ�Σ�Ҫ�߹���ͼ����д������������ͼ�ۼ���������EC���ӳ���BD�ڵ�M�����BMC=_________���æ���ʾ����
��1����BD=CE ��180�㩁2�� ��2��BD=kCE��90�㩁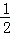 �� ��3��90��+
�� ��3��90��+ ��
��
���������������1����ͼ1��
��BD=CE���������£�
��AD=AE����ADE=����
���AED=��ADE=����
���DAE=180�㩁2��ADE=180�㩁2����
ͬ���ɵã���BAC=180�㩁2����
���DAE=��BAC��
���DAE+��BAE=��BAC+��BAE��
������BAD=��CAE��
�ڡ�ABD���ACE�У�
��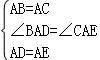 ��
��
���ABD�ա�ACE��SAS����
��BD=CE��
�ڡߡ�ABD�ա�ACE��
���BDA=��CEA��
�ߡ�BMC=��MCD+��MDC��
���BMC=��MCD+��CEA=��DAE=180�㩁2����
��2����ͼ2��
��AD=ED����ADE=����
���DAE=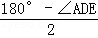 =90�㩁
=90�㩁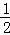 ����
����
ͬ���ɵã���BAC=90�㩁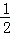 ����
����
���DAE=��BAC��
���DAE+��BAE=��BAC+��BAE��
������BAD=��CAE��
��AB=kAC��AD=kAE��
��AB��AC=AD��AE=k��
�ڡ�ABD���ACE�У�
��AB��AC=AD��AE=k����BDA=��CEA��
���ABD�ס�ACE��
��BD��CE=AB��AC=AD��AE=k����BDA=��CEA��
��BD=kCE��
�ߡ�BMC=��MCD+��MDC��
���BMC=��MCD+��CEA=��DAE=90�㩁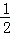 ����
����
�ʴ�Ϊ��BD=kCE��90�㩁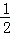 ����
����
��3����ͼ��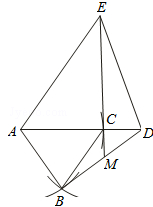
��AD=ED����ADE=����
���DAE=��AED=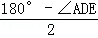 =90�㩁
=90�㩁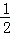 ����
����
ͬ���ɵã���BAC=90�㩁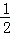 ����
����
���DAE=��BAC������BAD=��CAE��
��AB=kAC��AD=kAE��
��AB��AC=AD��AE=k��
�ڡ�ABD���ACE�У�
��AB��AC=AD��AE=k����BAD=��CAE��
���ABD�ס�ACE��
���BDA=��CEA��
�ߡ�BMC=��MCD+��MDC����MCD=��CED+��ADE=��CED+����
���BMC=��CED+��+��CEA=��AED+��=90�㩁 ��+��=90��+
��+��=90��+ ����
����
�ʴ�Ϊ��90��+ ����
����
���㣺���������ε��ж������ʣ�ȫ�������ε��ж������ʣ���ͼ-��ת�任��
���������⿼����ȫ�������ε��ж������ʣ������ε���ǵ����ʣ����������ε��ж������ʣ���ͼ����ת�任���ۺ��Խ�ǿ����һ���Ѷȣ�����ȫ�������Ƶ�����������������ڶ��ʿ��Խ�����һ�ʵ�˼·�����������������ֿ������յڶ��ʵ�����������������dz������ݽ������õ�һ���ǹؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ||||||||
(
|
| ||||||||
(
|
| ||||||||
(
|
| 1 |
| a+b+c |
| 1 |
| b+c-a |
| 1 |
| c+a-b |
| 1 |
| c-a-b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�������ѧ��Ԫ���Ų��Ծ�-���Ƶ��ж�����⣨�����棩 ���ͣ������
��֪����C��A��D��ͬһ��ֱ���ϣ���ABC=��ADE=�����߶�BD��CE���ڵ�M��
��1����ͼ1����AB=AC��AD=AE
�����߶�BD��CE��������������ϵ����˵�����ɣ�
�����BMC�Ĵ�С���æ���ʾ����
��2����ͼ2����AB=BC=kAC��AD=ED=kAE�����߶�BD��CE��������ϵΪ��_________������BMC=��_________�����æ���ʾ����
��3���ڣ�2���������£��ѡ�ABC�Ƶ�A��ʱ����ת180�㣬�ڱ���ͼ��������ת���ͼ�Σ�Ҫ�߹���ͼ����д������������ͼ�ۼ���������EC���ӳ���BD�ڵ�M�����BMC=��_________�����æ���ʾ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com