
分析 根据根的判别式可得出△=$(\sqrt{3})^{2}$+(2-4n)$\sqrt{3}$+52,再根据方程有一个整数根且n为正整数即可得出关于n的一元一次方程,解方程即可得出结论.
解答 解:在方程x2-($\sqrt{3}$+1)x+$\sqrt{3}$n-6=0中,
△=$[-(\sqrt{3}+1)]^{2}$-4×($\sqrt{3}$n-6)=28+(2-4n)$\sqrt{3}$=3+(2-4n)$\sqrt{3}$+25=$(\sqrt{3})^{2}$+(2-4n)$\sqrt{3}$+52.
∵方程有一个整数根,且n为正整数,
∴2-4n=-10,
解得:n=3.
点评 本题考查了根的判别式,根据方程有一个整数根结合根的判别式找出关于n的一元一次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
 已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG.
已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
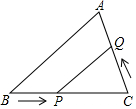 如图,在△ABC中,∠C=90°,BC=8cm,4AC-3BC=0,点P从B点出发,沿BC方向以2cm/s的速度移动,点Q从C点出发,沿CA方向以1cm/s的速度移动,若P、Q分别从B、C同时出发,经过多少秒时,△CPQ与△CBA相似?
如图,在△ABC中,∠C=90°,BC=8cm,4AC-3BC=0,点P从B点出发,沿BC方向以2cm/s的速度移动,点Q从C点出发,沿CA方向以1cm/s的速度移动,若P、Q分别从B、C同时出发,经过多少秒时,△CPQ与△CBA相似?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 3,5,2 | B. | 3,2,2 | C. | 2,3,5 | D. | 1,2,5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com