
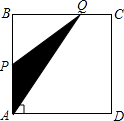
 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )| A. | 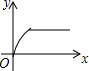 | B. | 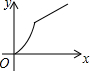 | C. | 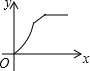 | D. | 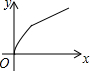 |
分析 根据题意,分两种情况:(1)当动点Q在BC边上运动时;(2)当动点Q在CD边上运动时;然后根据三角形的面积的求法,分类讨论,求出y与x之间函数关系式,进而判断出y与x之间函数关系图象的是哪个即可.
解答 解:(1)如图1,当动点Q在BC边上运动时,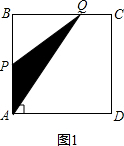 ,
,
∵4÷3=$\frac{4}{3}(秒)$,
∴动点Q从点B运动到点C向右的时间是$\frac{4}{3}$秒,
∵AP=2x,BQ=3x,
∴y=2x×3x÷2=3x2(0<x$≤\frac{4}{3}$),
∴抛物线开口向上;
(2)如图2,当动点Q在CD边上运动时,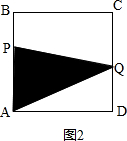 ,
,
∵(8+4)÷3=4(秒),4-$\frac{4}{3}=\frac{8}{3}(秒)$,
∴动点Q从点C运动到点D需要的时间是$\frac{8}{3}$秒,
∵AP=2x,BC=4,
∴y=2x×4÷2=4x($\frac{4}{3}$<x≤4),单调递增,
综上,可得
y=$\left\{\begin{array}{l}{{3x}^{2}(0<x≤\frac{4}{3})}\\{4x(\frac{4}{3}<x≤4)}\end{array}\right.$,
∴能大致表示y与x之间函数关系图象的是: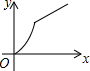 .
.
故选:B.
点评 (1)此题主要考查了动点问题的函数图象,考查了函数解析式的求法,以及分类讨论思想的应用,要熟练掌握.
(2)此题还考查了三角形的面积的求法,要熟练掌握,解答此题的关键是熟练掌握三角形的面积公式.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
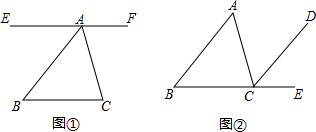
科目:初中数学 来源: 题型:填空题
 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
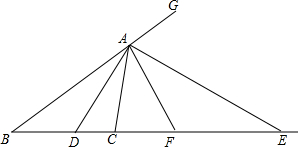 如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证:
如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙钟 | 4 | -3 | -1 | -2 | 1 | -2 | 2 | -2 | 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com