
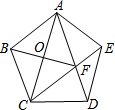
 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2. 分析 首先根据菱形的判定方法,判断出四边形ABCF是菱形,再根据菱形的性质,即可判断出AC⊥BF;然后根据勾股定理,可得OB2+OC2=BC2,据此推得AC2+BF2=4CD2即可.
解答 解:∵五边形ABCDE是正五边形,
∴AB∥CE,AD∥BC,
∴四边形ABCF是平行四边形,
又∵AB=BC=CD=DE=EA,
∴四边形ABCF是菱形,
∴AC⊥BF,
∴OB2+OC2=BC2,
∵AC=2OC,BF=2OB,
∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,
又∵BC=CD,
∴AC2+BF2=4CD2.
故答案为:AC2+BF2=4CD2.
点评 (1)此题主要考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.
(2)此题还考查了勾股定理的应用:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,正在播广告,是必然事件 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 某同学连续10次抛掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30% | |
| D. | 从一个只装有白球的缸里摸出一个球,摸出的球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
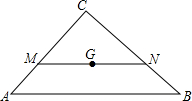 已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )
已知△ABC中,G是三角形的重心,AB=$\frac{15}{2}$,过点G的直线MN∥AB,交AC于M,BC于N,则MN的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
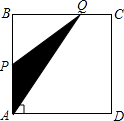 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )| A. |  | B. | 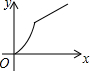 | C. | 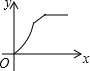 | D. | 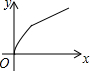 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com