
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有( )
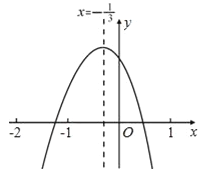
A.2个 B.3个 C.4个 D.5个
科目:初中数学 来源: 题型:
【题目】为给同学们创造更好的读书条件,学校准备新建一个长度为L的度数长廊,并准备用若干块带有花纹和没有花纹的两种规格、大小相同的正方形地面砖搭配在一起,按如图所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.6m.
(1)按图示规律,第一图案的长度L1=m;第二个图案的长度L2=m.
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln之间的关系.
(3)当走廊的长度L为36.6m时,请计算出所需带有花纹图案的瓷砖的块数及瓷砖总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。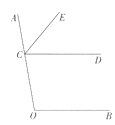
(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE= , ∠COF= ![]() ∠COB。
∠COB。
(理由: )
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠。
(理由: )
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将n个边长都为1cm的正方形按如图所示的方法摆放,点A1 , A2 , …,An分别是正方形对角线的交点,则n个正方形重叠形成的重叠部分的面积和为( )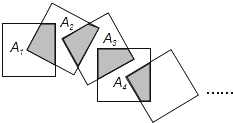
A.![]() cm2
cm2![]()
B.![]() cm2
cm2![]()
C.![]() cm2
cm2![]()
D.( ![]() )ncm2
)ncm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所示是二次函数y=ax2+bx+c图象的一部分,图象过点A(5,0),对称轴为直线x=1,下列结论中错误的是( )
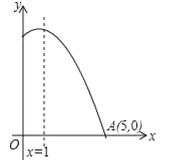
A.abc>0
B.当x<1时,y随x的增大而增大
C.a+b+c>0
D.方程ax2+bx+c=0的根为x1=﹣3,x2=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.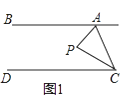
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.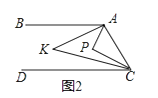
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.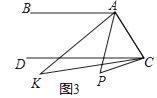
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com