
【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.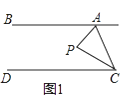
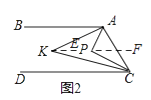
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.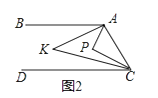
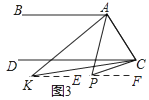
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.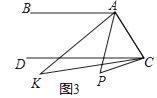
【答案】
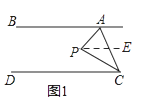
(1)解:如图1,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=∠BAP,∠CPE=∠DCP,
∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;
(2)解:∠AKC= ![]() ∠APC.
∠APC.
理由:如图2,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠AKE=∠BAK,∠CKE=∠DCK,
∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP+∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK+∠DCK= ![]() ∠BAP+
∠BAP+ ![]() ∠DCP=
∠DCP= ![]() (∠BAP+∠DCP)=
(∠BAP+∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC= ![]() ∠APC;
∠APC;
(3)解:∠AKC= ![]() ∠APC.
∠APC.
理由:如图3,过K作KE∥AB,
∵AB∥CD,
∴KE∥AB∥CD,
∴∠BAK=∠AKE,∠DCK=∠CKE,
∴∠AKC=∠AKE﹣∠CKE=∠BAK﹣∠DCK,
过P作PF∥AB,
同理可得,∠APC=∠BAP﹣∠DCP,
∵∠BAP与∠DCP的角平分线相交于点K,
∴∠BAK﹣∠DCK= ![]() ∠BAP﹣
∠BAP﹣ ![]() ∠DCP=
∠DCP= ![]() (∠BAP﹣∠DCP)=
(∠BAP﹣∠DCP)= ![]() ∠APC,
∠APC,
∴∠AKC= ![]() ∠APC.
∠APC.
【解析】(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;(2)过K作KE∥AB,平行公理的推理可得到KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义得出∠BAK+∠DCK=![]() ∠BAP+
∠BAP+![]() ∠DCP,进而可得到问题的答案;
∠DCP,进而可得到问题的答案;
(3)过K作KE∥AB,依据平行公理的推理可得到KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠AKE-∠CKE=∠BAK-∠DCK,同理可得,∠APC=∠BAP-∠DCP,再根据角平分线的定义,得出∠BAK-∠DCK=![]() ∠BAP-
∠BAP-![]() ∠DCP=
∠DCP=![]() (∠BAP-∠DCP)=
(∠BAP-∠DCP)=![]() ∠APC,进而得到∠AKC=
∠APC,进而得到∠AKC=![]() ∠APC.
∠APC.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).


科目:初中数学 来源: 题型:
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有( )
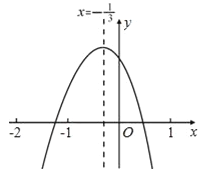
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着空气质量的恶化,雾霾天气现象增多,危害加重.森林是“地球之肺”,每年能为人类提供大约28.3亿吨的有机物,28.3亿可用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小方格边长为1个单位,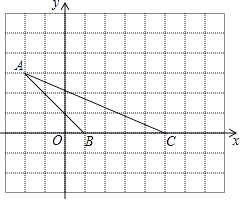
(1)请写出△ABC各点的坐标.
(2)求出S△ABC .
(3)若把△ABC向上平移2个单位,再向右平移2个单位△A′B′C′,在图中画出△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌的共享自行车企业为了解工作日期间地铁站附近的自行车使用情况,做到精确投放,于星期二当天对荔湾区A、B、C三个地铁站该品牌自行车后使用量进行了统计,绘制如图1和图2所示的统计图,根据图中信息解答下列问题: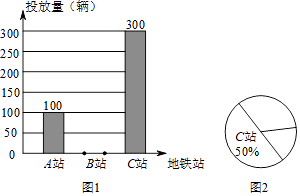
(1)该品牌自行车当天在该三个地铁站区域投放了自行车辆.
(2)请补全图1中的条形统计图;求出地铁A站在图2中所对应的圆心角的度数.
(3)按统计情况,若该品牌车计划在这些区域再投放1200辆,估计在地铁B站应投入多少辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
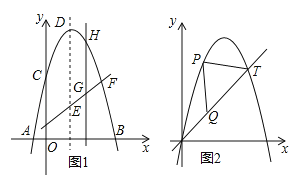
【题目】如图1所示,已知抛物线![]() 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,![]() =5:6?
=5:6?
(3)图2所示的抛物线是由![]() 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中的错误的是( ).
A、一组邻边相等的矩形是正方形
B、一组邻边相等的平行四边形是菱形
C、一组对边相等且有一个角是直角的四边形是矩形
D、一组对边平行且相等的四边形是平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com