
 如图,在正方形ABCD和正方形CEFG中,点B、C、E在同一条直线上,点M是边AD的中点,已知AB=a,CE=b(a<b).
如图,在正方形ABCD和正方形CEFG中,点B、C、E在同一条直线上,点M是边AD的中点,已知AB=a,CE=b(a<b).分析 (1)作辅助线,将△MGE分成了两个三角形,分别求DM和DN的长即可;
(2)代入求值即可.
解答 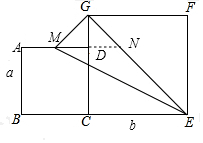 解:(1)延长MD交EG于N,
解:(1)延长MD交EG于N,
∵四边形ABCD为正方形,
∴DC=AB=AD=a,AD∥BC,
同理得:GC=CE=b,
∵M是AD的中点,
∴MD=$\frac{1}{2}$AB=$\frac{1}{2}$a,
∵DN∥CE,
∴△GDN∽△GCE,
∴$\frac{DN}{CE}=\frac{GD}{GC}$,
∴$\frac{DN}{b}=\frac{b-a}{b}$,
∴DN=b-a,
∴S△GME=S△GMN+S△MNE=$\frac{1}{2}$MN•DG+$\frac{1}{2}$MN•CD=$\frac{1}{2}$MN•CG=$\frac{1}{2}$($\frac{1}{2}$a+b-a)×b=$\frac{1}{2}{b}^{2}$-$\frac{1}{4}$ab;
(2)当a=3cm,b=5cm时,
S△GME=$\frac{1}{2}$×52-$\frac{1}{4}$×3×5=$\frac{35}{4}$,
答:△GME的面积为$\frac{35}{4}$.
点评 本题考查了正方形的性质、三角形的面积、相似三角形的性质和判定以及代入求值问题,本题三角形面积的求法有很多种:比如割补法、连接CM等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com