
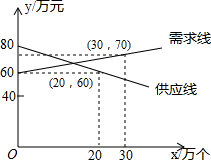
 某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡?
某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡? 分析 先求得供应线与需求线的函数关系式,然后将两个关系式联立组成方程组求解即可.
解答 解:设供应线的解析式为y=kx+80,将x=20,y=60代入得:20k+80=60,
解得:k=-1,
∴供应线的解析式为y=-x+80.
设需求线的解析式为y=k1x+60.将x=30,y=70代入得:30k1+60=70,解得k1=$\frac{1}{3}$.
∴需求线的解析式为y=$\frac{1}{3}$x+60.
将y=$\frac{1}{3}$x+60与y=-x+80联立得:$\left\{\begin{array}{l}{y=-x+80}\\{y=\frac{1}{3}x+60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=15}\\{y=65}\end{array}\right.$,
65÷15=4$\frac{1}{3}$(元).
答:计划生产这种计算器15万个,每个的价格为4$\frac{1}{3}$元.
点评 本题主要考查的是一次函数的解析式,求得两个函数的解析式是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
 等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.
等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com