
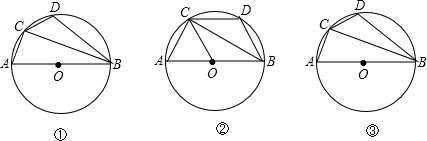
分析 (1)由AC=CD,可知∠ABC=∠CBD=20°,由AB是⊙O的直径,可知∠ACB=90°,根据直角三角形两锐角互余可求出∠A的大小;
(2)由AC=CD,可知∠AOC=2∠ABC=∠ABD,可得出OC∥BD,又OC=BD,所以四边形OCDB是平行四边形,由OC=OB,所以四边形OCDB是菱形;
(3)连接OC,作OE⊥BD,AF⊥OC,OH⊥AC,在△AOC中,根据勾股定理和三角形面积不变性,求出AF,易证AF=OE,根据勾股定理求出BE,则BD=2BE.
解答 解:(1)∵AC=CD,
∴∠ABC=∠CBD=20°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=70°;
(2)∵AC=CD,
∴∠AOC=2∠ABC=∠ABD,
∴OC∥BD,
又∵OC=BD,
∴四边形OCDB是平行四边形,
∵OC=OB,
∴四边形OCDB是菱形;
(3)如答图③,连接OC,作OE⊥BD,AF⊥OC,OH⊥AC,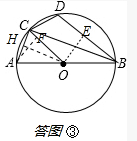 ∵AB=4,
∵AB=4,
∴OC=OA=2,
∵OH⊥AC,AC=1,
∴AH=$\frac{1}{2}$,
在Rt△AHO中,OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=$\frac{\sqrt{15}}{2}$,
∵AC•OH=OC•AF,
∴$\frac{\sqrt{15}}{2}$=2AF,
∴AF=$\frac{\sqrt{15}}{4}$,
∵OE⊥BD,AF⊥OC,
∴∠AFO=∠OEB=90°,
在△AOF和△OBE中,
$\left\{\begin{array}{l}{∠AFO=∠OEB}\\{∠AOF=∠OBE}\\{OA=OB}\end{array}\right.$
∴△AOF≌△OBE,
∴OE=AF=$\frac{\sqrt{15}}{4}$,
∴BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=$\frac{7}{4}$,
∴BD=2BE=$\frac{7}{2}$.
点评 本题主要考查了圆周角定理及其推论、菱形的判定与性质、勾股定理、垂径定理的综合运用,第3小题是本题的难点,通过辅助线构造高线和垂径定理的条件是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
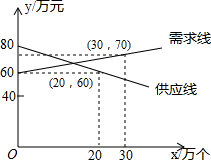 某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡?
某电子厂家经过市场调查发现,某种计算器的供应量x1(万个)与价格y1(万元)之间的关系和需求量x2(万个)与价格y2(万元)之间的关系如图所示,如果你是这个电子厂的厂长,你会计划生产这种计算器多少万个?每个售价多少元?才能使市场达到供需平衡?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
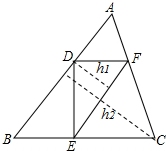 如图所示,D、E、F分别在△ABC的边上,DF∥BC,EF∥AB,如果AD:DB=1:2,则△DEF的高h1与△ABC的高h2的比h1:h2等于( )
如图所示,D、E、F分别在△ABC的边上,DF∥BC,EF∥AB,如果AD:DB=1:2,则△DEF的高h1与△ABC的高h2的比h1:h2等于( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com